Gráficos de control
Los procesos industriales implican la participación de una gran cantidad de elementos (capital humano, maquinaria, materia prima), lo que hace de los mismos procesos altamente complejos que deben ser evaluados, de manera constante, para garantizar que los resultados esperados se cumplan. En este contexto, se utilizan diversas herramientas que permiten gestionar este aspecto de la empresa, entre ellas los gráficos de control.
Los gráficos de control son una de las herramientas más importantes dentro del ejercicio analítico de un proceso, con el fin de garantizar la calidad de los productos manufacturados de acuerdo a unos estándares establecidos. En este artículo, te explicaremos de qué se tratan, cuáles son sus tipos, cómo hacer uno y te brindaremos instrumentos útiles para el desarrollo de los mismos.
¿Qué es un gráfico de control?
Un gráfico de control, también denominado diagrama de control o diagrama de Shewart, es una representación visual de la variación de los resultados de un proceso respecto al tiempo. En general, se trata de una herramienta para la evaluación de la calidad de los procedimientos llevados a cabo como parte de la etapa productiva de una empresa.
Este tipo de gráfico es, en realidad, un gráfico de líneas que emplea parámetros estadísticos, como la desviación estándar, para representar la diferencia del resultado obtenido respecto al resultado esperado.
Las empresas, generalmente, establecen un estándar (conocido, en este caso, como Línea central) para la producción de sus bienes. Sin embargo, no es posible que este se cumpla, pues durante un proceso, existen una gran cantidad de factores que pueden influir sobre los resultados del mismo.
Por lo anterior, también se estiman unos márgenes dentro de los cuales, esta variación es aceptable. Estos se conocen como Límite Superior de Control (LSC o UCL), por sus siglas en inglés) y Límite Inferior de Control (LIC o LCL). Mientras que los resultados se encuentren dentro de estos límites, se considera que estos son óptimos. Por el contrario, si se exceden a los mismos, se evidencia una falla grave sobre el proceso.
¿Para qué sirven las gráficas de control?
Las gráficas de control hacen parte de las herramientas de control estadístico de procesos, un campo de la estadística que se enfoca en la inspección y verificación de los resultados de cada etapa productiva para garantizar la calidad de los mismos. Es por esta razón que este tipo de gráficos brindan tanta utilidad para los supervisores y gerentes, pues les permiten detectar patrones negativos e implementar, de manera rápida, soluciones.
La mejora continua de una empresa depende, en gran medida, de la implementación de estas herramientas. Los gráficos de control facilitan la interpretación, análisis y comprensión de los estados de los procesos que se estén llevando a cabo en un momento dado. Además, cuentan con la rigurosidad matemática que brinda la rama de la estadística descriptiva
Fuentes de variación en un proceso
Durante un proceso influyen una gran cantidad de factores, que pueden afectar, tanto positiva como negativamente, al mismo y pueden causar una variación en sus resultados. Es por esta razón que es importante identificar aquellos que son parte del proceso y, por lo tanto, difícilmente pueden ser eliminados; y aquellos que son externos al mismo. Estos se dividen en:
Causas comunes
Las causas comunes, denominadas en algunas ocasiones como causas aleatorias, son aquellas que hacen parte del proceso en sí. Es decir, el inicio del mismo, implica la aparición de estos factores, por lo que no es posible evitar sus efectos sobre el desarrollo productivo de la empresa.
Estas son circunstanciales o eventuales, por lo que no se puede determinar el momento exacto en que influyen sobre el proceso ni aquel en que aparecen, pero se puede suponer su existencia. Sin embargo, no implican un alto grado de riesgo para la producción de la empresa.
Causas especiales
Las causas especiales, a menudo llamadas causas asignables, son aquellas cuyo origen no está intrínsecamente relacionado al proceso, y su aparición se debe a factores externos o que no están determinados por la producción. En estos casos, es más fácil conocer la razón por la que están afectando la etapa productiva, pues son factores específicos.
Estas causas producen efectos negativos sobre el proceso y sus resultados, y son la principal fuente de un alto grado de variación sobre los productos manufacturados y sus respectivas medidas.
Tipos de gráficos de control
Los gráficos de control se clasifican en distintas clases, según el tipo de dato a considerar dentro del análisis. Cabe destacar que los datos cuantitativos se dividen en datos discretos y continuos, y es a partir de esta división que se tienen los siguientes tipos de gráficos de control:
Gráficas de control por variables
Los gráficos de control por variables representan el comportamiento de los datos cuantitativos continuos, es decir, aquellos que representan una magnitud física (altura, peso, dimensión, tiempo). A su vez, estos se clasifican en:
Gráfica x – R (promedios y rangos)
Los gráficos x-R son aquellos que representan el comportamiento de los datos respecto al promedio (x) de los mismos y al rango (R) en el que se encuentran. En estos casos, los datos se encuentran agrupados en diferentes conjuntos (ya sea el número de registro, fecha, día, entre otros) y se busca evaluar los diferentes valores según otros criterios.
Generalmente, este supone un único gráfico, en el que se representan los promedios obtenidos en función del criterio evaluado, por ejemplo, el tiempo. Sin embargo, también se puede diseñar un gráfico para promedios o rangos, el cual es el más utilizado, e independientemente un gráfico de rangos.
Cabe destacar que el rango se debe calcular mediante la fórmula Xmax – Xmin, es decir, el mayor de los datos menos el menor.
Para calcular los límites se debe aplicar la siguiente fórmula:
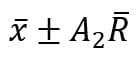
Donde:
- X con barra superior: es el promedio muestral.
- A: es una constante (más abajo, encontrarás una tabla de constantes para diseñar gráficos en Excel).
- R con barra superior: es el promedio de los rangos.
Se debe tener en cuenta que, al calcular el límite superior de control, se realiza una suma, mientras que al determinar el límite inferior de control, se hace una resta. Esto aplica para todas las demás fórmulas del resto de gráficos de control.
Gráfica x – s (promedios y desviación estándar)
Los gráficos x-s representan la varianza de los resultados a partir del promedio de los mismos y de la desviación estándar entre ellos. En general, el proceso de construcción del gráfico es similar al del gráfico x-r. Sin embargo, en este caso se debe aplicar la fórmula:
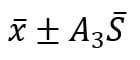
Donde S es la desviación estándar. A menudo, también se emplea la letra sigma minúscula (σ) para simbolizar esta medida estadística.
Gráfica x – R (medianas y rangos)
Los gráficos x-R para medianas y rangos son similares a los gráficos de promedios y rangos. Sin embargo, como lo indica su nombre, en este caso se deben calcular las medianas de cada subgrupo de datos y, posteriormente, calcular el promedio entre ellas. Las medianas son el valor medio de un conjunto de datos ordenados de menor a mayor.
Gráfica x – R (lecturas Individuales y rangos)
Las gráficas de lecturas u observaciones individuales y rangos se utilizan para el control sobre procesos que implican largas etapas de producción, por lo que requieren un análisis distinto al de las gráficas x – R normales.
En este caso, el gráfico para las lecturas individuales se construye a partir de los límites calculados de la siguiente manera:
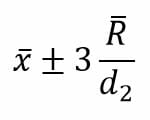
Donde d es una constante.
Por otro lado, para calcular los límites del gráfico de rangos, se deben aplicar las siguientes fórmulas para determina el límite superior y el límite inferior, respectivamente:
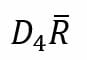
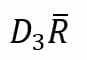
Donde D es igualmente una constante.
Gráficas de control por atributos
Los gráficos control por atributos se refieren a aquellos que representan la manera en que se comporta un conjunto de datos cuantitativos discretos, los cuales se tratan de cantidades (por ejemplo, la cantidad de personas que habitan una zona, número de manzanas de un árbol), cuyas unidades no se pueden dividir y, por lo tanto, se deben considerar como una parte entera.
En este tipo de gráfico de control, se busca determinar si un producto presenta las condiciones y características óptimas para considerar que es bueno o, por el contrario, defectuoso. Por esta razón, se denominan gráficos de control por atributos.
Estos gráficos se dividen en:
Gráfica p (porcentaje de unidades o procesos defectuosos)
La gráfica p se utiliza para conocer la proporción o porcentaje de procesos o unidades defectuosos respecto al total de los mismos. Para calcular esto, se debe dividir el número de productos con fallas entre el tamaño de la muestra, cuyo resultado es la variable p.
Finalmente, para calcular los respectivos límites, se debe aplicar la siguiente fórmula:
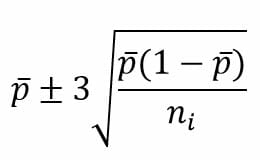
Donde n es el tamaño de la muestra.
Gráfica np (número de unidades o procesos defectuosos)
Los gráficos np se utilizan para representar el número de unidades defectuosas producidas durante un proceso. Para calcular la variable np, se debe dividir la suma resultante de las cantidades de unidades defectuosas de cada observación, entre el tamaño muestral, es decir, el número de observaciones.
Hecho lo anterior, se calculan los límites de la siguiente manera, teniendo en cuenta que el límite superior es una suma y el inferior, una resta:
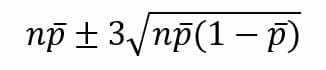
Gráfica c (número de defectos por área de oportunidad)
La gráfica c se emplea para realizar un control a partir del número de defectos por área de oportunidad o, lo que es lo mismo, por producto o unidad. En este caso, cada unidad es evaluada con el fin de contabilizar la cantidad de fallas que presenta y concluir si se trata de un producto defectuoso o no.
Para calcular c se debe dividir el número total de defectos encontrados en todos las unidades entre el número de observaciones.
Por último, se aplica la fórmula para calcular los límites:
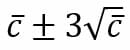
Gráfica u (porcentaje de defectos por área de oportunidad)
Los gráficos u permiten representar, visualmente, la variabilidad de los resultados de un proceso mediante la proporción o porcentaje de errores que presenta una unidad. Para calcular u, se debe dividir el número de defectos recopilado en cada una de las muestras entre el tamaño de esta última (Ci / ni).
Al calcular u, se puede aplicar la siguiente fórmula para calcular los respectivos límites:
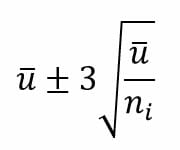
Cómo hacer un gráfico de control: Paso a paso
Hacer un gráfico de control requiere de seguir ciertos pasos para llevarlo a cabo correctamente. A continuación, te explicaremos cómo crear uno:
- Define el objetivo de la investigación: todos los procesos son diferentes, incluso si hacen parte de una misma empresa o una misma línea productiva. Por esta razón, es importante conocer, de manera previa, qué se quiere investigar, ya sea una etapa en específico o los resultados finales de la producción, así como las características físicas a tener en cuenta.
- Reúne la información necesaria: investiga cada unidad o proceso y registra sus resultados. Considera tener en cuenta el mayor conjunto de datos posible, con el fin de reducir el margen de error de la investigación. Asimismo, clasifica la información.
- Identifica el tipo de gráfico: puedes optar por utilizar uno u otro tipo de gráfico de control, siempre teniendo en cuenta si los datos que has manejado, durante el registro de los mismos, son continuos o discretos.
- Organiza los datos en una tabla: es recomendable, en cualquier tipo de análisis, organizar la información en una tabla, con el fin de clasificar y ordenar los datos, permitiendo utilizarlos correctamente durante la aplicación de las fórmulas.
- Realiza los respectivos cálculos: ten en cuenta que cada gráfico tiene unas fórmulas específicas, por lo que debes ser cuidadoso al realizar los cálculos.
- Gráfica cada uno de los puntos en un plano: dibuja un plano y gráfica cada uno de los valores resultantes a partir de los anteriores cálculos (como los límites y los diferentes resultados registrados en primera instancia). Finalmente, une los puntos formando las respectivas rectas y segmentos.
- Concluye: finalmente, identifica los puntos que se encuentran fuera de control, es decir, aquellos que superan los límites establecidos en el gráfico. A partir de esto, puedes emprender acciones para mejorar las circunstancias del proceso.
¿Cómo hacer un gráfico de control en Excel?
En el ámbito industrial, se suelen utilizar diferentes programas informáticos con el fin de realizar análisis más precisos y optimizar las tareas involucradas en los mismos. Microsoft Excel destaca en este contexto, tanto por las diversas funciones que ofrece para realizar cálculos, así como por las herramientas que permiten diseñar gráficos de distintos tipos.
En este apartado, te explicaremos cómo se hace un gráfico de control en Excel de manera rápida y sencilla. Solo sigue estas instrucciones:
En este caso, consideraremos los diferentes volúmenes de las piezas producidas por una empresa.
De acuerdo a la normativa de la empresa, los bloques que deben tener un volúmen de 2,5 centímetros cúbicos. Sin embargo, se presenta una variación en los resultados.
- Para calcular la media, se puede utilizar la función matemática PROMEDIO. Para ello, solo escribimos su sintaxis en la barra de fórmulas, seleccionando el rango de celdas que contienen los diferentes volúmenes registrados.
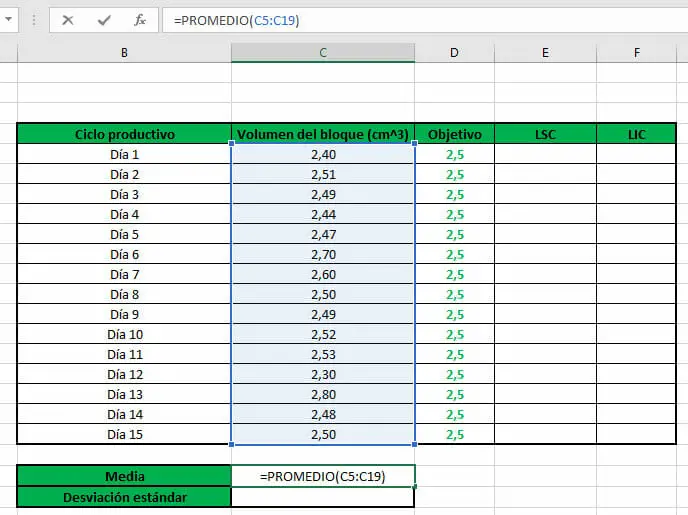
- La desviación estándar se puede calcular mediante la función estadística DESVEST. Al igual que en el paso anterior, únicamente se selecciona el conjunto de datos recopilado.
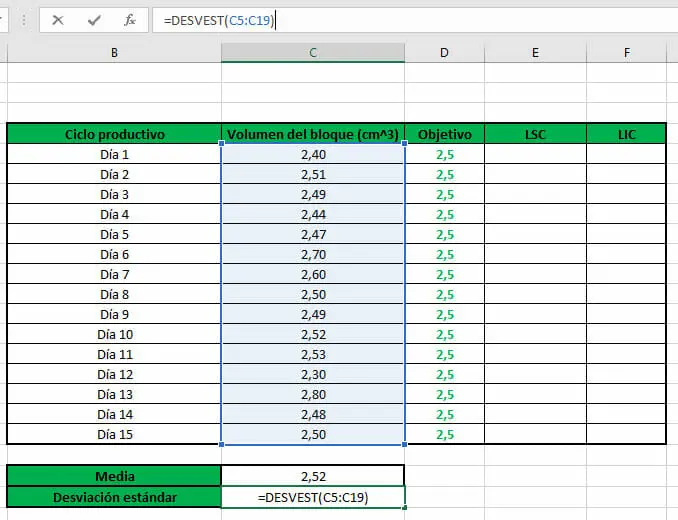
- En este momento, debemos calcular los respectivos límites dentro de los cuales se puede considerar que los resultados de la producción son óptimos:
- Al momento de calcular el Límite Superior de Control, debemos escribir la siguiente fórmula en Excel:
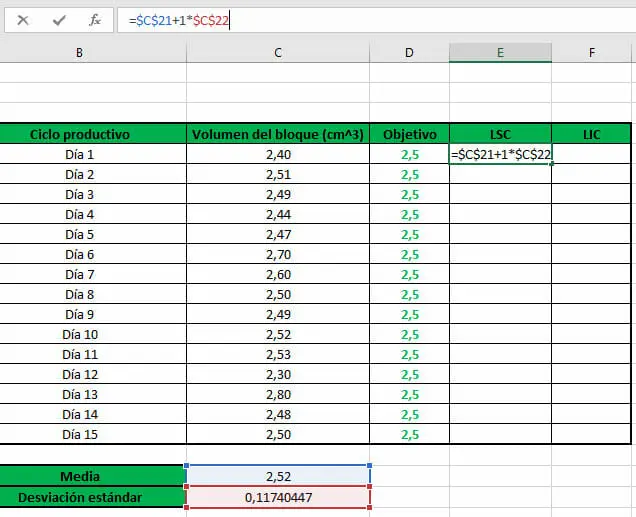
- Por último, calculamos el Límite Inferior de Control realizando la operación a continuación:
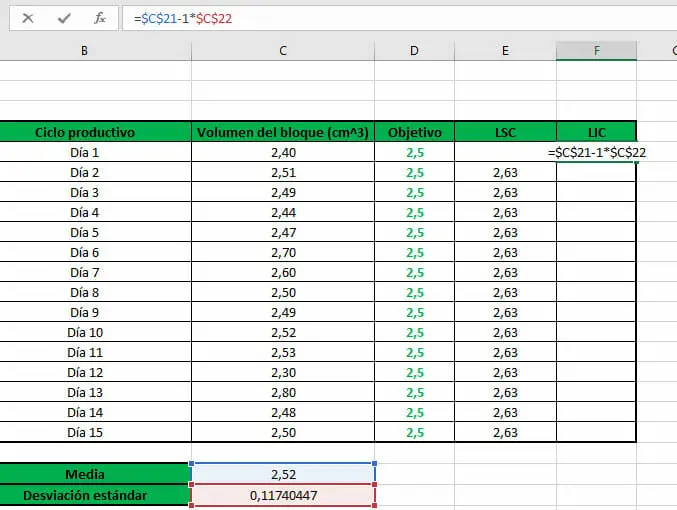
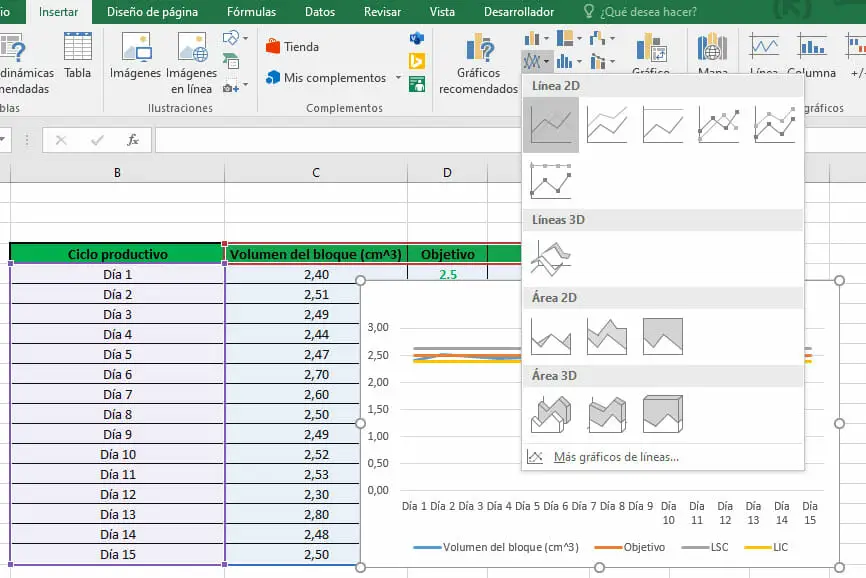
- Ahora, con el fin de graficar toda la información anteriormente establecida, nos dirigimos a la pestaña Insertar y, en la cinta de opciones, buscamos la sección Gráficos y seleccionamos un gráfico de líneas, una vez seleccionados los datos de la tabla.
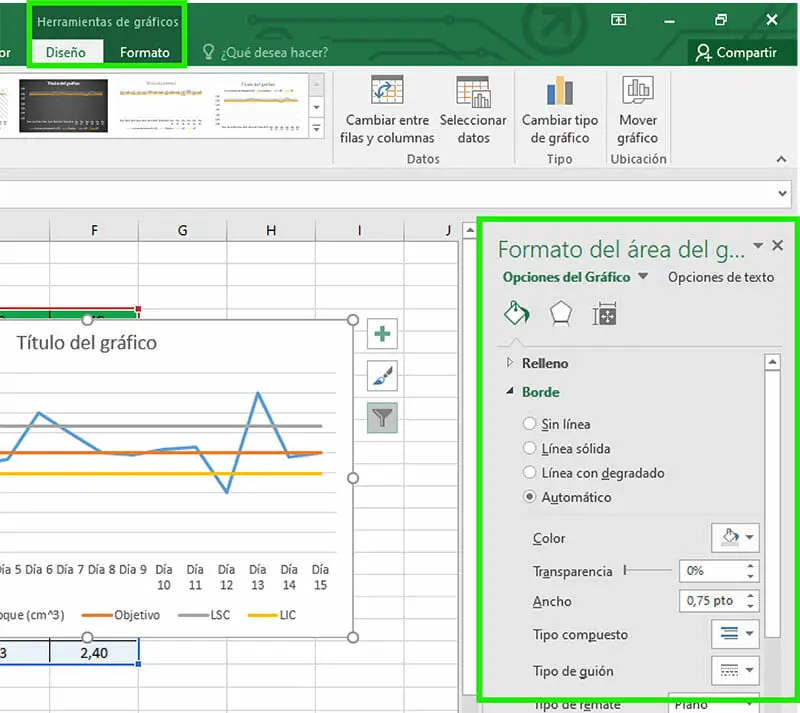
- Microsoft Excel permite personalizar los gráficos mediante diferentes herramientas. Podemos acceder a ellas a través de la sección Herramientas de gráficos, que se encuentra en la parte superior de la barra de herramientas, o haciendo doble click sobre el gráfico. En este último caso, se desplegará una sección en la parte derecha de la ventana de Excel.
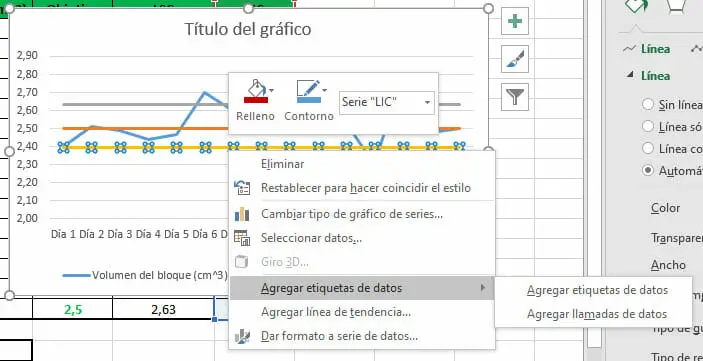
Puede resultar útil agregar etiquetas a las diferentes líneas de la gráfica, con el fin de conocer sus valores. Para ello, podemos hacer click derecho sobre la recta a etiquetar y seleccionar la opción Agregar etiquetas de datos.
Ejemplo gráfica de control
Una empresa de juguetería que se dedica a la producción de bloques o piezas de construcción, como parte de su gestión de calidad, ha registrado, durante 15 días, los diferentes volúmenes de las unidades producidas en ese intervalo de tiempo. Cabe mencionar que, de acuerdo a la normativa de la organización, esta magnitud debe ser igual a 8 centímetros cúbicos.
Al recopilar los datos, se ha realizado en siguiente gráfico de control:
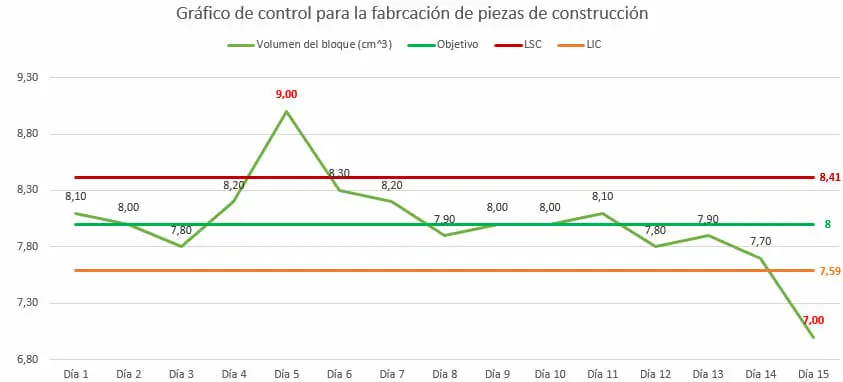
Como se puede observar, los resultados de la producción se han mantenido dentro de los límites aceptables, exceptuando los del día 5 y 15. Mientras que en el primero, las piezas presentaron un error mayor al LSC, en el último, estas redujeron su volumen.
De esta manera, la empresa puede emprender una investigación de las razones por las que esto ocurrió en dichos días, implementar estrategias para que esta situación no se repita y reducir posibles errores futuros.
La mejora continua de una empresa depende, fundamentalmente, de la gestión de calidad de sus procesos. Los gráficos de control son, por lo tanto, uno de los principales elementos para el progreso de un negocio. A partir de ellos, se pueden implementar diferentes estrategias, como las metodologías ágiles, o complementarse con otros diagramas, como el diagrama de Ishikawa, que permite identificar las causas de un problema.
Análisis e Interpretación de un gráfico de control
Como cualquier gráfico estadístico, los gráficos de control permiten visualizar el comportamiento de un conjunto de datos, facilitando su interpretación y análisis. Sin embargo, es necesario conocer algunos puntos para poder sacar conclusiones relevantes de este tipo de gráficos. A continuación, te explicaremos cómo hacerlo:
- Identifica los puntos fuera de control: si la curva excede algunos de los dos límites establecidos, se dice que, en dicho punto, el proceso estuvo fuera de control. A partir de esto, se pueden buscar las razones por las que esto ocurrió.
- Distingue las causas: generalmente, las variaciones de este tipo ocurren por causas especiales, por lo que se deben buscar las circunstancias que se presentaron durante la etapa de producción de la unidad en específico, con el fin de evitarlas en el futuro o implementar estrategias de mejora.
- Analizar comportamientos y patrones: la recurrencia de un resultado fuera de control puede deberse a una circunstancia repetitiva que, si no se soluciona, puede generar mayores fallos en el futuro. Por ejemplo, si se observa que el error es cíclico, o se presenta cada cierto tiempo, se puede hacer una revisión de ese momento en específico para conocer las causas que afectan al proceso.
Tabla de constantes para gráficos de control
En estadística y, en general, en cualquier campo relacionado a las matemáticas, se utilizan constantes de diversos tipos, las cuales se suelen considerar al momento de realizar una gran cantidad de cálculos. Sin embargo, en algunas ocasiones, estas pueden ser difíciles de recordar, por lo que es recomendable recurrir a una tabla que recopile toda la información necesaria para llevar a cabo las respectivas operaciones.
Para realizar un gráfico de control, es necesario aplicar diversas fórmulas en las cuales se debe considerar ciertas constantes. Por esta razón, puede ser bastante útil tener una tabla que incluya toda esta información y, a partir de la cual, se puedan hacer cálculos rápidos.
A continuación, encontrarás una tabla de constantes para gráficos de control, con todos los datos necesarios para realizar los respectivos cálculos. Solo debes descargarla ¡y listo!
Plantilla Gráfico de control y Calidad en Excel
Los procesos industriales deben ser supervisados constantemente, con el fin de garantizar unos resultados óptimos y, en consecuencia, el progreso incremental de la empresa. Los gráficos de control son una herramienta fundamental en este tipo de gestiones, y por esta razón, en Excel Para Todos, hemos desarrollado la Plantilla Gráfico de Control y de Calidad en Excel.
La Plantilla Gráfico de control y Calidad en Excel te permite diseñar gráficos de promedios o medias de manera rápida y sencilla. Solo debes registrar los datos en la tabla ¡y listo! Podrás diseñar, instantáneamente, un gráfico de control, con el que podrás evaluar la calidad de tus procesos y conocer si los resultados se encuentran en unos límites aceptables. ¡Es totalmente gratuita!