Medidas de tendencia central
Gran parte de la labor que abarca la estadística se enfoca en la descripción y representación de un conjunto de datos a través de tablas y gráficos estadísticos, con el fin de facilitar su posterior análisis. Sin embargo, durante este proceso también es necesario utilizar ciertos parámetros o medidas que permitan resumir dicha información. Unas de las más importantes son las medidas de tendencia central.
Las medidas de tendencia central son una de las medidas más importantes dentro de la investigación estadística, pues permiten agilizar el proceso analítico e interpretar, rápidamente, la naturaleza real de un conjunto de datos. En este artículo, te explicaremos todo lo que necesitas saber sobre este concepto.
¿Qué son las medidas de tendencia central?
Las medidas de tendencia central, también denominadas medidas de posición, son parámetros estadísticos, los cuales representan los valores centrales o más representativos de un conjunto de datos.
En general, hacen referencia al valor al que tienden, principalmente, los demás valores de un conjunto. De esta manera, describen la distribución central de dicho conjunto y resumen su comportamiento en un único dato.
En estadística descriptiva, las medidas de tendencia central hacen parte de los parámetros utilizados para describir un grupo de información, además de la distribución de frecuencias y las medidas de variabilidad.
¿Para qué sirven las medidas de tendencia central?
La principal utilidad de las medidas de tendencia central se relaciona a su capacidad de sintetizar, resumir y representar, con la mayor exactitud, un conjunto de datos en un solo número. A partir de este número se pueden llevar a cabo una gran cantidad de análisis interesantes para una investigación, tales como:
- Identificar errores o valores que difieran en extremo con la tendencia central.
- Establecer un rango de normalidad.
- Conocer la naturaleza de un conjunto de datos.
- Realizar comparaciones entre los distintos datos del conjunto y el valor central.
- Estudiar la distribución de los datos.
Importancia de las medidas de tendencia central en el análisis de datos estadísticos
Durante el análisis estadístico, es necesario tener una visión global o general de un conjunto de datos antes de someterlo a un análisis riguroso, con el fin de seleccionar los métodos más adecuados para cada caso. Así, la importancia de las medidas de tendencia central se encuentra en la resolución de dicha necesidad, brindando datos específicos que resumen el comportamiento o naturaleza de un objeto de estudio.
Además, reducen la dispersión de los datos, logrando obtener, de esta manera, valores más representativos y exactos. Aunque gran parte de su importancia radica en este aspecto, cabe destacar que las medidas de tendencia central son bastante sensibles a los valores extremos, por lo que, en algunos casos, es necesario realizar un análisis más cuidadoso.
Tipos de medidas de tendencia central
Las medidas de tendencia central se clasifican, principalmente, en tres clases, según el resultado que se desea obtener durante la evaluación de la población o la muestra. De esta manera, se puede determinar el valor que se presenta con mayor frecuencia dentro de un conjunto de datos, aquel que se encuentra justo en la mitad o, incluso, calcular el dato más representativo de todos. Veamos cuáles son estos tipos:
Promedio o Media (media aritmética)
El promedio, o media aritmética, es el valor más representativo de un conjunto de datos y matemáticamente se define como el cociente obtenido al dividir la suma de los valores entre el total de elementos del conjunto.
Es el tipo de medida de tendencia central más utilizado, pues permite observar, de manera general, la distribución o características propias de un conjunto de datos y, por lo tanto, conocer su naturaleza.
Cabe destacar que en este caso se habla de la media aritmética simple, es decir, aquella cuyos valores tienen el mismo peso. Por el contrario, cuando los valores guardan proporciones o pesos diferentes, es necesario aplicar una media aritmética ponderada.
Fórmula
La fórmula para calcular el promedio de un conjunto de datos es:
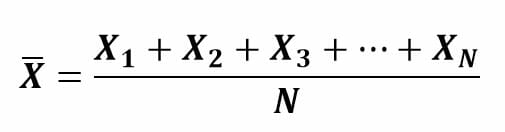
Donde:
- X: son cada uno de los datos que pertenecen a la población o muestra.
- N: número de datos de la población o muestra.
Ejemplo
Un breve ejemplo de una aplicación de la media aritmética o promedio es la siguiente: como parte de una investigación escolar, los estudiantes de un colegio deben recopilar las alturas de 8 de sus compañeros, con el fin de obtener un promedio de los mismos. Al hacerlo, se obtuvieron los siguientes datos:
| 1,72 | 1,70 | 1,80 | 1,89 | 1,95 | 1,75 | 1,70 | 1,79 |
A partir de estos datos, se puede calcular cuál es la altura más representativa del grupo. Así, al sumar las alturas se obtiene que:
1,72 + 1,70 + 1,80 + 1,89 + 1,95 + 1,75 + 1,70 + 1,79 = 14,3 metros.
Y al dividir dicho resultado con el total de estudiantes se tiene que:
14,3 / 8 = 1,79 metros.
Así, el promedio de las alturas de los estudiantes es de 1,79 metros. Es decir, es la altura a la que tienden la mayoría estudiantes según el total de datos.
Mediana
La mediana es el valor central, de un conjunto de datos ordenados (de menor a mayor), es decir, se encuentra en la mitad de dicho conjunto, tal que se puede definir que es aquel que es mayor que la primera mitad, pero menor que la segunda.
Fórmula
En realidad, el valor de la mediana se obtiene a partir de conocer su posición en el conjunto de datos, por lo que la fórmula relacionada a esta medida de tendencia central permite conocer dicha posición. Cabe destacar, entonces, dos casos:
- Cuando el número de datos del conjunto es impar: en este caso, el valor de la mediana es aquel que se encuentra justo en el centro del conjunto de datos. Su posición se puede conocer a través de la fórmula:
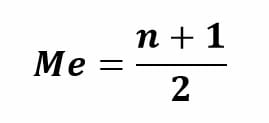
Donde n es el número de datos de la población o muestra.
- Cuando el número de datos del conjunto es par: aquí, se tienen dos valores centrales, entre los cuales se encuentra el valor real de la mediana. Su posición se puede conocer a través de la fórmula anterior. Dicha posición en realidad hace referencia a los dos datos mencionados.
Posteriormente, se promedian los valores de los dos datos centrales y, así, se obtiene, finalmente, el valor de la mediana.
Ejemplo
Para este ejemplo, consideraremos los siguientes pesos en kilos, una vez ya ordenados:
| 56,7 | 60,1 | 62,3 | 66,4 | 67,3 | 70,8 | 71,2 | 73,5 |
En este caso, el número de datos es par, por lo que, como se puede observar, no existe un valor central, por lo que es necesario considerar dos valores. Así, en primera instancia aplicamos la fórmula para conocer su posición:
(8 + 1) / 2 = 4,5.
Por lo tanto, los dos valores se encuentran en la posición 4 y la posición 5, que son los números enteros a los que se puede aproximar 4,5. Ahora, solo se deben promediar:
(66,4 + 67,3) / 2 = 66,85 kilos.
Es decir, la mediana de los datos recopilados es de 66,86 kilos.
Moda
La moda es el valor con mayor frecuencia entre un conjunto de datos, es decir, el que más número de veces se repite en una variable estadística. En este caso, la distribución de los valores se puede clasificar de tres maneras:
- Distribución unimodal: solo uno de los valores presenta la máxima de las frecuencias.
- Distribución bimodal: dos valores presentan la máxima frecuencia posible.
- Distribución multimodal: más de dos valores presentan una mayor frecuencia que el resto.
Fórmula
En general, no existe una fórmula para calcular la moda de un conjunto de datos, pues únicamente se trata de un proceso de observación o conteo, en el que se determina cuál de los datos es el que se repite el mayor número de veces. Sin embargo, cuando los datos se encuentran agrupados en intervalos ordenados o se tiene en cuenta una variable continua, entonces se debe aplicar la siguiente fórmula:
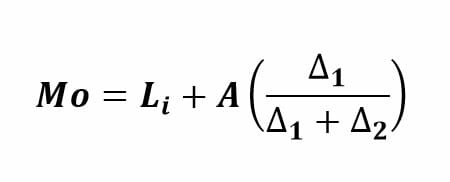
Donde:
- Li: es el límite inferior del intervalo.
- A: es la amplitud del intervalo.
- Δ1: es la diferencia entre la frecuencia absoluta entre el intervalo con mayor frecuencia y el anterior.
- Δ2: es la diferencia entre la frecuencia absoluta entre el intervalo con mayor frecuencia y el siguiente.
En este caso, se debe tener en cuenta que todos los elementos de la fórmula están relacionados a la clase de la moda, es decir, el intervalo de datos con mayor frecuencia absoluta.
Ejemplo
Para mayor comprensión de este último concepto, se realizará un ejemplo donde sea necesario aplicar la fórmula descrita. Así, se tienen agrupados en intervalos los siguientes datos:
| Intervalo | Frecuencia absoluta |
| 56 – 70 | 10 |
| 70 – 84 | 32 |
| 84 – 98 | 50 |
| 98 – 112 | 41 |
| 112 – 126 | 30 |
| 126 – 140 | 12 |
Como se puede observar, el intervalo con mayor frecuencia es aquel con límites de 84 a 98. Ahora, veamos los valores obtenidos para cada elemento:
- Li: 84.
- A: 98 – 84 = 14.
- Δ1: 50 – 32 = 18.
- Δ2: 50 – 41 = 9.
Al realizar los respectivos cálculos, se obtiene que la moda es 93,3.
¿Cómo calcular las medidas de tendencia central en Excel?
Microsoft Excel se utiliza en una gran cantidad de ámbitos profesionales y académicos, tales como la física, las matemáticas, la contabilidad, las finanzas y la estadística. Esto se debe a la amplia gama de herramientas y opciones que se pueden emplear para realizar los cálculos relacionados a cada una de estas ramas, tales como las funciones estadísticas o las funciones financieras.
En este caso, te enseñaremos a calcular los tres tipos de medidas de tendencia central utilizando las principales funciones estadísticas de Excel. Para ello, tomaremos en cuenta la lista de edades de un curso universitario.
Calcular la media en Excel
Para calcular la media aritmética en Excel, solo debes utilizar la función PROMEDIO, de la siguiente manera:
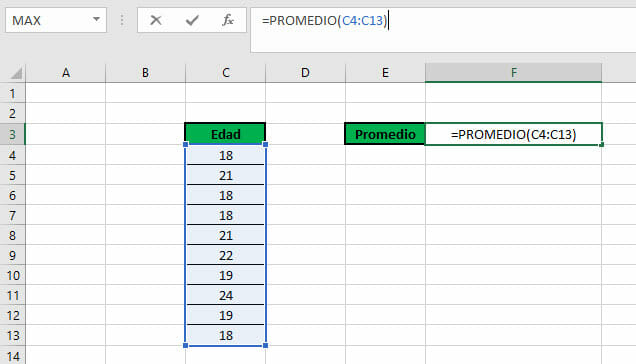
El resultado de dicha operación será 19,8 años.
Calcular la mediana en Excel
La mediana se puede calcular a través de la función MEDIANA, seleccionando los valores de la tabla, y escribiendo la sintaxis de la función en la barra de fórmulas de Excel:
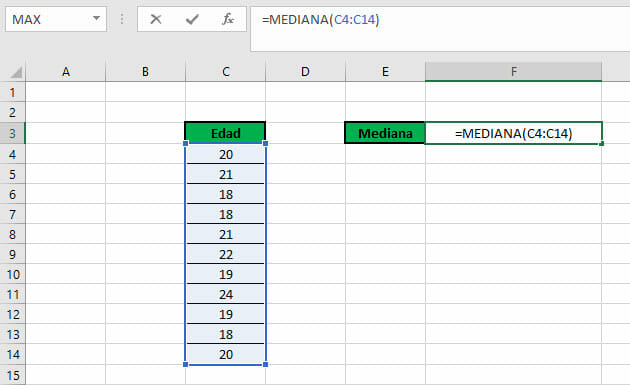
En este caso, la mediana es igual a 20 años. Aunque esto no se puede observar tal como se encuentra ordenada la tabla, la función MEDIANA realiza los cálculos pertinentes para brindar el resultado exacto de dicha medida.
Calcular la moda en Excel
Finalmente, para calcular la moda puedes utilizar la función MODA, como se muestra en la imagen:
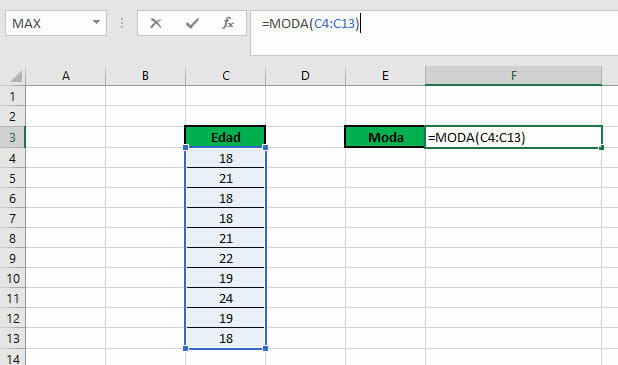
La edad que más se repite entre la lista de edades del curso universitario es 18 años, la cual equivale a la moda.
Conclusiones
La estadística descriptiva es una de las etapas fundamentales del análisis estadístico y se puede considerar, asimismo, la base para el desarrollo de una investigación. Gran parte de esta importancia se debe a las medidas de tendencia central, las cuales permiten sintetizar la información de un conjunto de datos en un valor único.
Este valor único brinda una visión global acerca del objeto de estudio, facilitando su análisis posterior y la comprensión de su naturaleza antes de empezar con un estudio profundo y riguroso del mismo.
Puedes complementar la información presentada en este artículo con los siguientes contenidos:
