Distribución de frecuencias
La estadística descriptiva es una de las primeras fases de una investigación estadística, pues consiste en realizar una descripción inicial de la población para que, posteriormente, se puedan extraer conclusiones acertadas respecto al estudio. Para ello, se utilizan diferentes magnitudes estadísticas, como las frecuencias, las cuales se deben organizar en una forma específica. Es aquí donde surge el concepto de distribución de frecuencias.
En este artículo, te explicaremos de qué se trata la distribución de frecuencias, cómo se clasifica y cómo se debe hacer una correctamente. Además, al final del mismo, te brindaremos una herramienta realmente útil para realizar este tipo de análisis estadísticos.
¿Qué es la distribución de frecuencias en estadística?
La distribución de frecuencias es un método mediante el cual los datos se organizan en categorías mutuamente excluyentes, es decir, que la existencia de una supone la inexistencia de la otra en un momento o circunstancias dadas. Así, cada categoría se relaciona con una frecuencia en específico y, de esta manera, se pueden realizar comparaciones entre las diferentes clases en las que se divide la población.
Esta distribución se lleva a cabo a través de tablas (conocidas como tablas de frecuencias), siendo la primera las columnas donde se ubican los datos de la variable estudiada y las demás, donde lo hacen las frecuencias que se relacionan a los mismos.
¿Para qué sirve la distribución de frecuencias?
La distribución de frecuencias resulta bastante útil como fase preliminar de una investigación estadística, en tanto que lo que se busca, como primera instancia, es hacer una clara descripción de la muestra. De esta manera, la información se puede organizar en tablas, facilitando el análisis de las frecuencias y permitiendo identificar la relación de los datos con cada una de las magnitudes estudiadas.
Tipos de distribución de frecuencias
Existen diversos tipos de frecuencias, lo que implica conocer cada uno de sus conceptos, así como los cálculos relacionados para realizar un correcto análisis de las mismas. De igual manera, cada una de ellas es importante para la interpretación final de los resultados de la investigación.
Distribución de frecuencia absoluta (fi)
La frecuencia absoluta es el número de veces que se repite un mismo dato en una variable. Es decir, es la recurrencia con que un fenómeno, suceso o característica aparece en la muestra estudiada. Para determinar dicha magnitud estadística, solo se debe realizar un conteo de los datos recopilados según la categoría a la pertenecen.
Es importante mencionar que la suma de las frecuencias absolutas debe ser igual al número de elementos de la muestra obtenida. De esta manera, se verifica que se hayan considerado todos los datos.
Distribución de frecuencia absoluta acumulada (Fi)
La frecuencia absoluta acumulada es la suma consecutiva de las frecuencias absolutas, de manera que cada una se suma con su anterior. Su fórmula es:
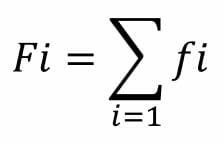
Distribución de frecuencia relativa (hi)
La frecuencia relativa es la proporción de la cantidad de veces que aparece un mismo dato en la muestra, respecto a los demás. En consecuencia, la suma de las frecuencias relativas es igual a la unidad, lo que se interpreta como el total. Para calcular esta magnitud estadística, simplemente se divide la frecuencia absoluta entre el tamaño muestral.
Distribución de frecuencia relativa acumulada (Hi)
La frecuencia relativa acumulada es aquella que se obtiene al sumar cada una de las frecuencias relativas, de manera consecutiva. Se interpreta, asimismo, como el porcentaje acumulado para cada uno de los datos de la variable. Su cálculo es el siguiente:
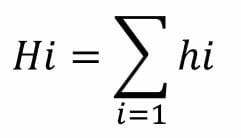
Distribución de frecuencia porcentual
La frecuencia porcentual es el porcentaje de veces que un mismo dato aparece en un conjunto, respecto al total. En realidad, se trata de una frecuencia relativa expresada, en este caso, de manera porcentual, por lo que simplemente se calcula multiplicando hi por 100.
¿Cómo hacer una distribución de frecuencias?
En general, para realizar una distribución de frecuencias, sólo es necesario tener en cuenta los siguientes pasos:
- Recopila y organiza los datos: en primera instancia, debes conocer la característica a estudiar (esto puede ser la altura de las personas, el número de ventas por día, entre otros). Posteriormente, se selecciona una muestra de la población a través de un muestreo estadístico y se organizan los datos en tablas.
- Diseña tu tabla de frecuencias: una vez se han organizado los datos, se diseña una tabla donde se incluyen los diferentes tipos de frecuencias. En la primera columna, se registran los valores de la variable estadística. Así, a cada uno de los datos le corresponde una frecuencia en específico.
- Determina la frecuencia absoluta: para esto, solo es necesario contar el número de veces que aparece cada uno de los datos en la muestra recopilada.
- Calcula la frecuencia relativa y porcentual: calculadas las frecuencias absolutas, simplemente se debe dividir cada una de estas entre el tamaño muestral, y su resultado se expresa tanto en decimal como en términos porcentuales.
- Calcula las frecuencias acumuladas: tanto para la frecuencia absoluta como para la relativa, se calculan sus respectivas frecuencias acumuladas. Solamente se deben sumar, de manera consecutiva, cada una de las frecuencias de los datos.
- Verifica los resultados totales: al final del ejercicio, se puede verificar si los totales corresponden al tamaño muestral de la investigación. Así, la suma de las frecuencias absolutas debe ser igual al número de elementos en la muestra, y la suma de las frecuencias relativas debe ser igual a 1.
Ejemplos de distribución de frecuencias
Los ejemplos pueden ilustrar, de mejor manera, cómo se debe realizar una distribución de frecuencias en la realidad. Por esta razón, en este apartado, te explicaremos dos casos en los que es necesario realizar un análisis de frecuencias, con el fin de que observes cómo se debe organizar los datos y realizar los cálculos:
Distribución de frecuencias para datos agrupados
Una distribución de frecuencias para datos agrupados se refiere a una tabla en donde los elementos de la muestra se organizan en intervalos. Esto se debe a que la característica medida se puede cuantificar mediante números decimales. Así, la altura, el peso, la velocidad, entre otras magnitudes físicas, se deben organizar a través de intervalos.
Te puede interesar consultar los siguientes artículos: Escala de medición y Variable continua.
Ahora, veamos un breve ejemplo: se desea conocer el tiempo que requiere la preparación de un plato cualquiera en un restaurante. Al realizar varias revisiones, se obtienen los siguientes tiempos (medidos en minutos):
| 9,5 | 10,7 | 15,4 | 12,8 | 9,7 | 14,4 |
| 13,3 | 13,5 | 15,1 | 14,9 | 10,8 | 11,9 |
Una vez se ha tomado la muestra, es necesario realizar los siguientes cálculos para diseñar la tabla de frecuencias:
- Rango (R): se trata de la diferencia entre el máximo de los valores de la muestra, y el mínimo. Su fórmula es Xmax – Xmin.
- Número de intervalos (K): se calcula a través de la regla de Sturges, la cual indica que 1 + 3,322logn (donde n es el tamaño muestral) es igual al número de intervalos en que se debe dividir la distribución de frecuencias. Se debe aproximar a un número entero.
- Amplitud (Ci): es decir, la distancia que debe tener el intervalo entre su límite inferior y su límite superior. Se calcula mediante R / K.
- Marca de clase (Xi): es el promedio del intervalo medido. Se calcula de la siguiente manera: (Límite inferior + Límite superior) / 2.
Explicado esto, ahora podemos proceder con el diseño de la tabla. Calculemos, entonces, cada uno de los elementos necesarios:
- R: 15,4 – 9,5 = 5,9.
- K: 1 + 3,322log(12) = 5.
- Ci: 5,9 / 5 = 1,2.
| Intervalo | Xi | fi | Fi | hi | Hi | hi% |
| [9,5 – 10,7) | 10,1 | 2 | 2 | 0,167 | 0,167 | 16,7% |
| [10,7 – 11,9) | 11,3 | 2 | 4 | 0,167 | 0,334 | 16,7% |
| [11,9 – 13,1) | 12,5 | 2 | 6 | 0,167 | 0,501 | 16,7% |
| [13,1 – 14,3) | 13,7 | 2 | 8 | 0,167 | 0,668 | 16,7% |
| [14,3 – 15,5) | 14,9 | 4 | 12 | 0,333 | 1 | 33,3% |
| Totales | 12 | 1 | 100% |
Para calcular las frecuencias absolutas, solo es necesario considerar aquellos datos que abarquen cada uno de los intervalos especificados.
Distribución de frecuencias con datos no agrupados
Una distribución de frecuencias con datos no agrupados se refiere a aquella cuyos elementos son unidades, es decir, números enteros. Así, la variable estudiada se puede medir en cantidades exactas. Ejemplo de esto es el número de personas que habitan en una casa o la cantidad de hermanos por persona.
Te puede interesar leer: Variable discreta.
Veamos el siguiente caso: se desea conocer el número de mascotas que habitan por hogar en un edificio de una zona residencial. Después de haber realizado la correspondiente recopilación de los datos, se obtiene lo siguiente:
| 1 | 3 | 3 | 2 | 1 | 3 | 1 | 3 | 5 | 5 |
| 4 | 3 | 2 | 2 | 2 | 3 | 4 | 4 | 3 | 2 |
| 4 | 4 | 5 | 3 | 5 | 5 | 2 | 3 | 2 | 1 |
En este caso, simplemente se debe identificar las categorías en las que se deben relacionar cada uno de los datos, tal y como se muestra en la siguiente tabla de frecuencias:
| Variable | fi | Fi | hi | Hi | hi% |
| 1 | 4 | 4 | 0,133 | 0,133 | 13,3% |
| 2 | 7 | 11 | 0,233 | 0,366 | 23,3% |
| 3 | 9 | 20 | 0,3 | 0,666 | 30% |
| 4 | 5 | 25 | 0,167 | 0,833 | 16,7% |
| 5 | 5 | 30 | 0,167 | 1 | 16,7% |
| Totales | 30 | 1 | 100% |
Análisis de la distribución de frecuencias
La distribución de frecuencias es, sin embargo, solo una de las primeras fases en las que se divide una investigación estadística. Por sí sola, no brinda la información suficiente para realizar conclusiones acertadas respecto a la población estudiada. Es por esta razón que se hace necesario aplicar ciertas medidas y herramientas para interpretar el conjunto de datos analizado. A continuación, te explicamos de cuáles se tratan.
Medidas de tendencia central
Las medidas de tendencia central son aquellas que determinan aquellos valores centrales o más típicos en un conjunto de datos. En esencia, estas indican hacia qué valor tienden la mayoría de los datos. Así, proporcionan una descripción resumida de la parte central de la distribución de datos y permiten tener una idea general de su comportamiento utilizando un solo número representativo.
Medidas de dispersión
Las medidas de dispersión son parámetros estadísticos que miden el grado de separación o agrupación de los datos en un conjunto, con respecto a su promedio o media aritmética. Básicamente, estas indican cuán dispersos o cercanos están los datos respecto al valor central.
Herramientas de visualización
Existen diversas herramientas de visualización de la distribución de frecuencias que permiten diseñar gráficos estadísticos, capaces de facilitar el análisis de los datos. Microsoft Excel, por ejemplo, es uno de los softwares más usados debido a que, en su gran abanico de herramientas, permite al usuario crear diagramas de barras o diagramas de columnas, histogramas, polígonos de frecuencias, entre otros.
Calculadora de distribución de frecuencias en Excel
¿Deseas realizar un análisis de distribución de frecuencias rápido, sencillo y de manera agradable? ¡Pues la Calculadora de distribución de frecuencias en Excel es para ti! Solo necesitas agregar los datos de la muestra ¡y listo! Automáticamente se calcularán las respectivas frecuencias para que puedas generar resultados seguros y precisos. Descárgala ¡es gratis!