Polígono de frecuencia
Los investigadores y científicos utilizan, a menudo, una gran cantidad de gráficos estadísticos para visualizar el comportamiento de un conjunto de datos y facilitar su comprensión e interpretación. La distribución de frecuencias también se puede representar mediante estas gráficas, siendo una de las más útiles el polígono de frecuencia.
Un polígono de frecuencia es ampliamente utilizado durante el análisis estadístico de una población o muestra, debido a que se puede realizar fácilmente y se pueden obtener resultados rápidos y precisos. A continuación, te explicaremos todo lo que necesitas saber sobre este gráfico y cómo puedes hacer uno de manera sencilla.
¿Qué es un polígono de frecuencia?
Un polígono de frecuencia es un gráfico que representa la frecuencia (es decir, el número de veces que se repiten unos datos estadísticos) a través de una serie de puntos interconectados mediante unas líneas o segmentos de recta. La altura de estos es el valor de dicha magnitud estadística.
Los polígonos de frecuencia se utilizan, principalmente, para representar la distribución de frecuencia de los datos de una variable continua, como lo puede ser una magnitud física o cualquier otro valor que acepte un número decimal. Por lo tanto, dichos datos se deben organizar en intervalos. Sin embargo, también se puede utilizar para variables discretas, las cuales abarcan, únicamente, números enteros.
Al momento de dibujar un polígono de frecuencias, se debe haber realizado, previamente, un histograma. En general, este gráfico se trata de un conjunto de barras cuya altura equivale a la frecuencia de los datos. Así, los puntos de intersección de las líneas se disponen en los extremos superiores de dichas barras.
Aunque, por lo general, los puntos de intersección se dibujan, simplemente, en la mitad del lado superior de la barra, es recomendable tener en cuenta las marcas de clase, es decir, el punto medio del intervalo.
En algunas ocasiones, se suele dibujar, en un solo gráfico, tanto el polígono de frecuencia como el histograma. No obstante, este último se puede utilizar únicamente como referencia para realizar el polígono de manera individual.
Características del polígono de frecuencias
- Se utiliza, en general, para variables continuas.
- Se asemeja a un gráfico de líneas.
- El área bajo la curva es igual al total de los datos de la muestra o población.
- Se dibuja a partir de un histograma.
- Representa la frecuencia absoluta y la frecuencia relativa de un conjunto de datos.
- Las intersecciones que unen a los segmentos de recta se ubican en las marcas de clase de los intervalos formados.
Propósito y utilidad del polígono de frecuencia en el análisis de datos
La utilidad del polígono de frecuencia radica en que permite comparar la distribución de frecuencias de un conjunto de datos, al facilitar la visualización de frecuencias mayores y frecuencias menores. Además, facilita observar la progresión de los datos, según ciertos criterios como los puede ser el tiempo, o simplemente la secuencia de los mismos de menor a mayor.
Sin embargo, una de sus características más importantes y donde se marca una verdadera diferencia respecto a otros gráficos es la representación de las marcas de clase, permitiendo identificar, con mayor precisión, el promedio de los intervalos y su ubicación en la gráfica.
Relación entre el polígono de frecuencia y el histograma
El polígono de frecuencia y el histograma son dos de los gráficos estadísticos más utilizados para representar la distribución de frecuencia de una variable estadística, y se encuentran estrechamente relacionados entre sí.
Esta relación se debe a que, para realizar un polígono de frecuencia se debe haber dibujado, de manera previa y necesaria, un histograma. Es decir, el polígono de frecuencia es una extensión de este último, que puede aportar cierta información relevante que no se puede observar fácilmente en el histograma.
En general, estos dos tipos de gráficos se complementan mutuamente, pues el histograma permite realizar comparaciones fácilmente, mientras que el polígono de frecuencia permite visualizar la progresión o patrón de los datos.
¿Cómo hacer una gráfica de polígono de frecuencia?
Al momento de realizar un polígono de frecuencia y, en general, cualquier otro tipo de gráfico, se deben tener en cuenta los siguientes pasos:
1: Organización de los datos
Una de las primeras etapas del método estadístico es la organización de los datos en diversas tablas, con el fin de ordenar y clasificar a los mismos y facilitar su graficación. En este caso, estos se deben organizar en una tabla de frecuencia.
Es importante que tengas en cuenta el tipo de variable, pues en uno u otro caso, se deben utilizar ciertas tablas específicas, que implican, asimismo, ciertas operaciones. A continuación, te explicamos estas consideraciones:
- Tabla de datos no agrupados: este tipo de tabla se utiliza para variables discretas, y solo se deben organizar los datos de manera ordenada, ya sea de menor a mayor o viceversa (véase Escala de medición).
- Tabla de datos agrupados: esta tabla se utiliza para variables continuas, cuyos datos se deben agrupar en intervalos. Por lo tanto, es necesario establecer cuántos intervalos se deben tener en cuenta, la amplitud de los mismos, entre otros datos.
En caso de que no sepas que es una tabla de datos agrupados o no sepas cómo hacerla, te invitamos a visitar nuestro artículo Tabla de frecuencia, donde te explicamos, de manera sencilla, cómo diseñar una.
2: Determinación de las frecuencias absolutas o relativas
Durante el análisis de distribución de frecuencia, se deben tener en cuenta dos tipos: la frecuencia absoluta y la frecuencia relativa:
- Frecuencia absoluta: es el número de veces que se repite un dato en una variable. Implica, únicamente, una revisión y conteo de los datos de la muestra o población.
- Frecuencia relativa: es la proporción de la frecuencia absoluta de un dato respecto al total de frecuencias. Su fórmula es fi / n, donde fi es la frecuencia absoluta y n, el número de datos del conjunto.
¡Y listo! Con estos datos puedes empezar a graficar el polígono de frecuencia teniendo en cuenta lo siguiente.
3: Representación gráfica
El primer paso para dibujar un polígono de frecuencia es haber dibujado, previamente, un histograma. En general, solo debes considerar la frecuencia de cada uno de los datos o intervalos y dibujar las columnas teniendo en cuenta que la altura de las mismas debe ser igual a dicha frecuencia.
Ahora, es momento de graficar el polígono de frecuencia, teniendo en cuenta estas consideraciones:
- Determina las marcas de clase: es decir, el promedio entre el límite inferior y el límite superior del intervalo en cuestión. Este se considera como el punto medio del intervalo.
- Ubica los puntos: estos se deben ubicar en la mitad de la parte superior de la columna del intervalo, representando, así, la marca de clase correspondiente.
- Conecta los puntos: finalmente, conecta las puntos dibujados mediante segmentos de recta.
Ejemplos de polígonos de frecuencias
Aquí, te enseñaremos un ejemplo práctico para que comprendas, de mejor manera, la aplicación de un polígono de frecuencia en una investigación y su utilidad. En este caso, se busca representar la frecuencia de consumo del servicio de gas en kilovatios por hora (kWh). Así, se realizó la siguiente tabla de datos agrupados:
| Intervalos (kWh) | Marcas de clase |
| [168.5, 237.575) | (168.5 + 237.575) / 2 = 203.0375 |
| [237.575, 305.65) | (237.575 + 305.65) / 2 = 271.6125 |
| [305.65, 375.725) | (305.65 + 375.725) / 2 = 340.6875 |
| [375.725, 444.8) | (375.725 + 444.8) / 2 = 410.2625 |
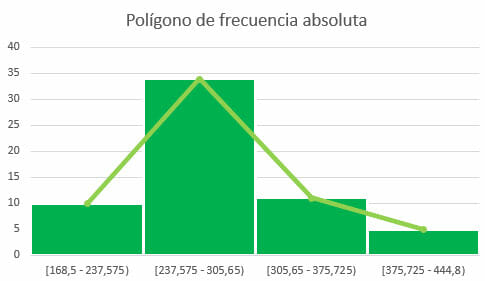
Polígono de frecuencia absoluta
Para determinar la frecuencia absoluta de un intervalo, sólo es necesario contar los datos de la muestra que se encuentran en el mismo. Para este ejemplo, consideraremos las siguientes frecuencias absolutas:
| Intervalos (kWh) | Marcas de clase | Frecuencia absoluta |
| [168.5, 237.575) | (168.5 + 237.575) / 2 = 203.0375 | 10 |
| [237.575, 305.65) | (237.575 + 305.65) / 2 = 271.6125 | 34 |
| [305.65, 375.725) | (305.65 + 375.725) / 2 = 340.6875 | 11 |
| [375.725, 444.8) | (375.725 + 444.8) / 2 = 410.2625 | 5 |
Así, al momento de diseñar el polígono, solo se deben ubicar los puntos que intersectan los segmentos de recta según la frecuencia absoluta, tal como se muestra en la siguiente imagen:
Polígono de frecuencia relativa
La frecuencia relativa de un intervalo es igual a dividir la frecuencia absoluta del mismo entre el total de frecuencias absolutas. En este caso, se obtiene la siguiente tabla de frecuencias:
| Intervalos (kWh) | Marcas de clase | Frecuencia absoluta | Frecuencia relativa |
| [168.5, 237.575) | (168.5 + 237.575) / 2 = 203.0375 | 10 | 0,17 |
| [237.575, 305.65) | (237.575 + 305.65) / 2 = 271.6125 | 34 | 0,57 |
| [305.65, 375.725) | (305.65 + 375.725) / 2 = 340.6875 | 11 | 0,18 |
| [375.725, 444.8) | (375.725 + 444.8) / 2 = 410.2625 | 5 | 0,08 |
| Total | 60 | 1 |
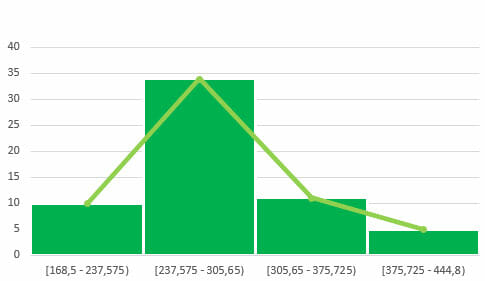
El procedimiento para graficar un polígono de frecuencia es similar al anterior e, incluso, el resultado será parecido. En este caso, solo se debe tener en cuenta los valores de las frecuencias relativas:
Pasos para realizar una gráfica de polígono de frecuencia en Excel
La labor estadística implica, en primera instancia, la organización de los datos en tablas, con el fin de facilitar el análisis de los mismos y su posterior graficación. Todas estas tareas se pueden realizar, de manera rápida y sencilla, en Microsoft Excel. Aquí, te mostraremos cómo utilizar esta herramienta para realizar un polígono de frecuencia en unos cuantos pasos:
- Una vez organizados los datos en una tabla, dirígete a la pestaña Insertar, ubicada en la barra de herramientas de Excel.
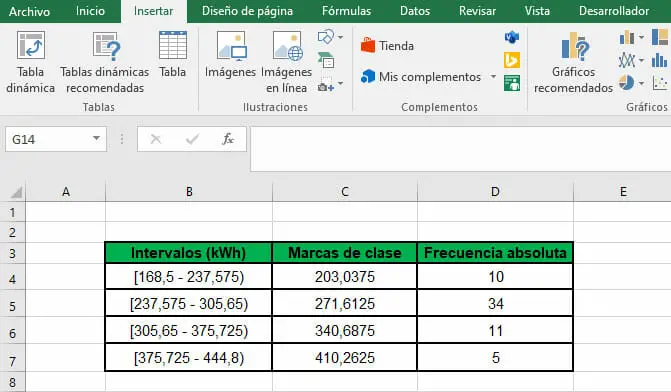
- Seleccionando las frecuencias de los intervalos escoge, en el apartado de Gráficos, una Columna agrupada.
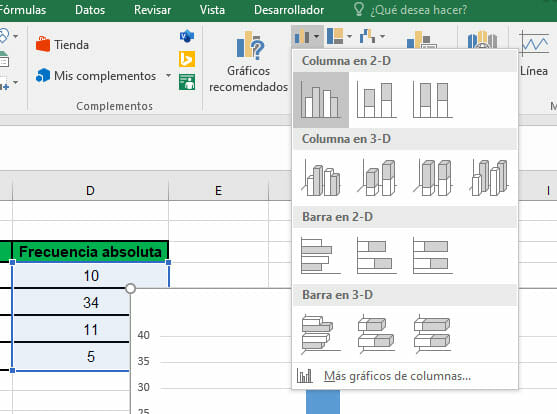
- Ahora, haz clic derecho sobre el gráfico y, luego, sobre la opción Seleccionar datos.
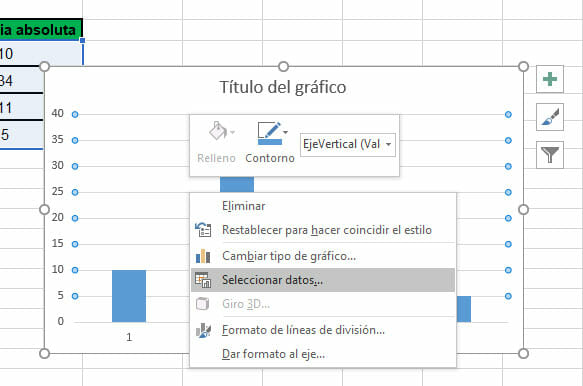
- Una ventana denominada Seleccionar origen de datos aparecerá en tu pantalla. Haz clic sobre el botón Editar y, en el nuevo recuadro, selecciona la columna que contiene los intervalos. Finalmente, apreta Aceptar.
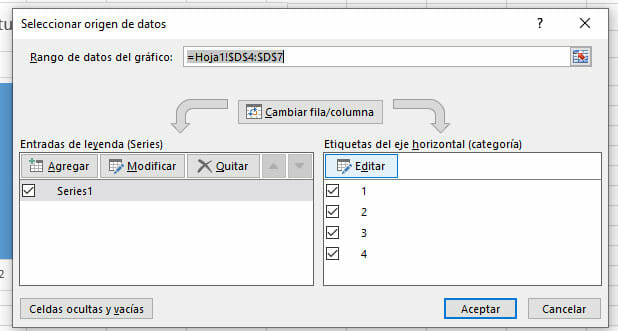
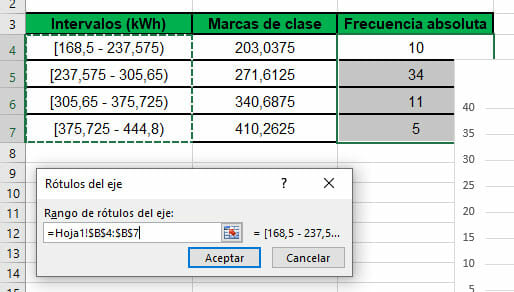
- En esta misma ventana, haz clic en Agregar y selecciona, en Valores de serie, nuevamente el rango de celdas que contiene las frecuencias absolutas.
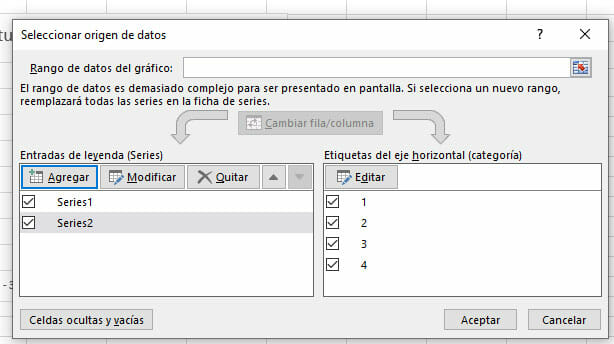
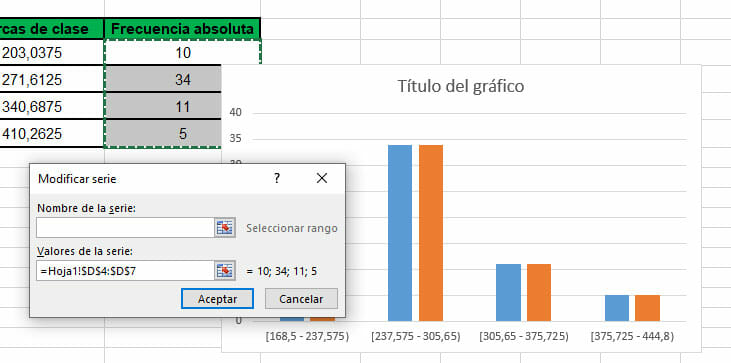
Por último, oprime Aceptar.
- Dirígete, nuevamente, a la pestaña Insertar. Ahora, selecciona, únicamente, las columnas de color naranja y selecciona un gráfico de líneas. Esto convertirá a las barras en segmentos de recta interconectados.
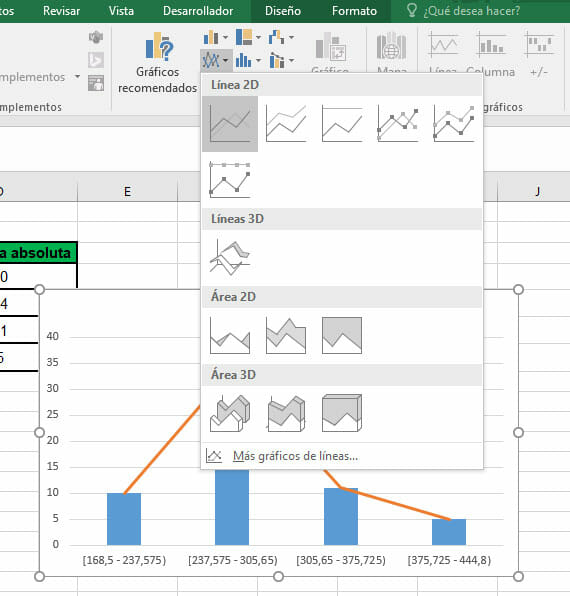
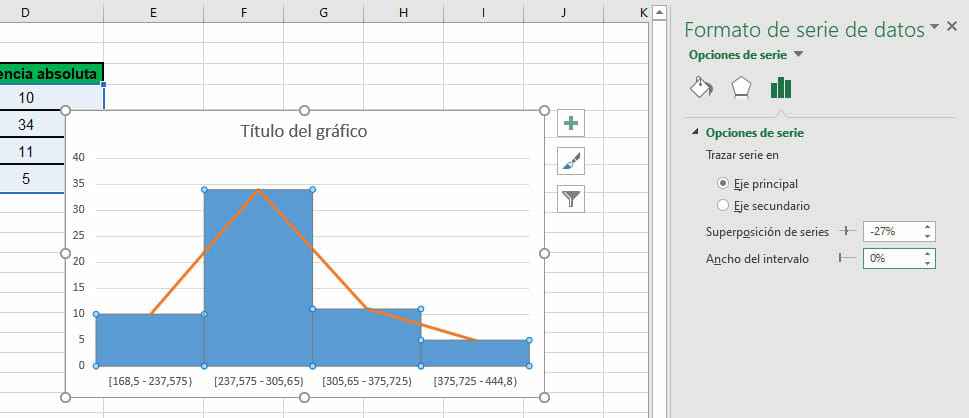
- Para que un histograma sea correcto, las columnas deben estar juntas. Para corregir esto, se debe hacer doble clic sobre el gráfico, activando un nuevo menú en la parte derecha de la ventana de Excel. Si haces clic, asimismo sobre las barras, puedes activar las Opciones de serie. Allí, debes modificar el Ancho del intervalo a 0%.
- Finalmente, en esta misma ventana, puedes personalizar tu polígono de frecuencia modificando los colores del gráfico.
Conclusiones y recomendaciones
Los gráficos estadísticos son una parte fundamental de la estadística, y gran parte de la labor relacionada a este campo se basa en la representación gráfica de grandes bloques de información. Así, tanto el polígono de frecuencia, como el histograma, el diagrama de barras o diagrama de columnas, son elementos necesarios para realizar una correcta investigación estadística y lograr los objetivos establecidos.
En especial, el polígono de frecuencia es una extensión útil de las demás gráficas utilizadas para representar la distribución de frecuencia, pues permite visualizar la progresión característica de un comportamiento específico, tal como se puede hacer con una función.
Puedes complementar lo que has aprendido en este artículo a través de los siguientes contenidos, donde tratamos diversos temas relacionados a la estadística:
