Frecuencia relativa
Entre los análisis estadísticos se encuentran los análisis de frecuencias, los cuales permiten obtener información relevante respecto a la repetición de un hecho en un contexto determinado. A partir de esto, los investigadores pueden inferir el comportamiento futuro de una población e implementar estrategias. Dentro de estos análisis, se tienen en cuenta diferentes magnitudes, siendo una de ellas la frecuencia relativa.
La frecuencia relativa es uno de los tipos de frecuencia más importantes y aporta información que se debe tener en cuenta para la evaluación de la población y la muestra. En este artículo, te explicaremos de qué se trata, cómo se calcula, cuál es su gráfica y te enseñaremos algunos ejemplos.
¿Qué es la frecuencia relativa?
La frecuencia relativa es una magnitud, utilizada en estadística, que indica la proporción o fracción de la cantidad de veces que ocurre un fenómeno o evento respecto a los demás. Esta cantidad se denomina frecuencia absoluta. En otras palabras, es el porcentaje que representa a un dato estadístico frente al total de la población o muestra.
El total de las frecuencias relativas representa la unidad, es decir, 1, pues cada una de ellas representa, únicamente, una parte del total de las frecuencias. Esto también se puede interpretar como que la suma de las frecuencias relativas es igual al 100%. Cuando estos valores se expresan en porcentajes se habla de frecuencia porcentual.
La distribución de frecuencias, de la que hace parte la frecuencia relativa, es uno de los parámetros más importantes de la estadística descriptiva. Esta permite comparar diversos grupos y la recurrencia de sus acciones o de los fenómenos que se presentan durante un periodo de tiempo.
Símbolo de la frecuencia relativa
En las tablas de frecuencia, así como en las fórmulas, el símbolo que representa a la frecuencia relativa es h¡. Aunque esto puede variar dependiendo de los autores, la mayoría de textos y fuentes utilizan dicho símbolo para referirse a esta magnitud estadística. El subíndice i, por su parte, representa el número de la frecuencia evaluada.
Fórmula de la frecuencia relativa
La fórmula de la frecuencia relativa se expresa, de forma literal, como el resultado de la división entre la frecuencia absoluta y el tamaño muestral o de la población:
hi = fi / n.
Con lo anterior, se busca hallar la proporción de la frecuencia absoluta respecto al total de los datos estadísticos recopilados. Por lo tanto, es necesario que, antes de calcular la frecuencia relativa, se hayan calculado las respectivas frecuencias absolutas.
¿Cómo calcular la frecuencia relativa?
Los datos estadísticos involucrados en una investigación se clasifican en dos tipos de variables, los cuales se deben tener en cuenta antes de diseñar una tabla de frecuencias o realizar cualquier tipo de análisis. Estos tipos son:
- Variables discretas: son números enteros que representan la cantidad de un conjunto de unidades. Por ejemplo, el número de páginas de un libro o la cantidad de mascotas de una familia.
- Variables continuas: son números decimales o fracciones que representan, generalmente, una magnitud física, como lo puede ser la altura o el peso. Estas se deben agrupar en intervalos semicerrados (cerrados por la izquierda y abiertos por la derecha).
Dependiendo del tipo de variable, la tabla de frecuencias se diseña de una u otra manera.
Una vez explicado lo anterior, se procede con lo siguiente:
- Diseñar la tabla de frecuencias, ordenando los datos de menor a mayor, en caso de que sean variables cuantitativas o cualitativas ordinales. Asimismo, se tienen en cuenta las diferentes frecuencias.
- Calcular las frecuencias absolutas, mediante un recuento de los datos.
- Aplicar la fórmula hi = fi / n para cada una de las frecuencias.
- Comprobar que la suma de las frecuencias relativas obtenidas sea igual a 1.
Ejemplos de frecuencia relativa
Los ejemplos y los ejercicios de aplicación pueden brindar una mayor claridad frente a la importancia de este concepto, así como de la manera en que se debe aplicar en cualquier caso. Por esta razón, te enseñaremos dos ejemplos para que puedas comprender, de mejor manera, cómo se calcula esta magnitud para cada tipo de variable.
Ejemplo de frecuencia relativa con variable discreta
El Ministerio de Salud de un país, como parte de un estudio de salubridad, ha emprendido una investigación respecto al número de personas que han sido diagnosticadas con neumonía, durante un intervalo de tiempo de 5 años. Al realizar la recolección de los datos, se ha obtenido lo siguiente:
| Año 1 | Año 2 | Año 3 | Año 4 | Año 5 |
| 2000 | 5000 | 1000 | 500 | 4000 |
Los profesionales, posteriormente, diseñan la siguiente tabla de frecuencias:
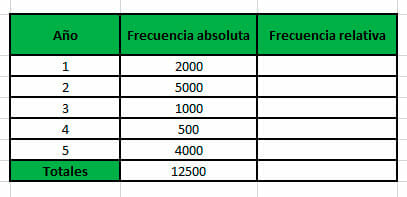
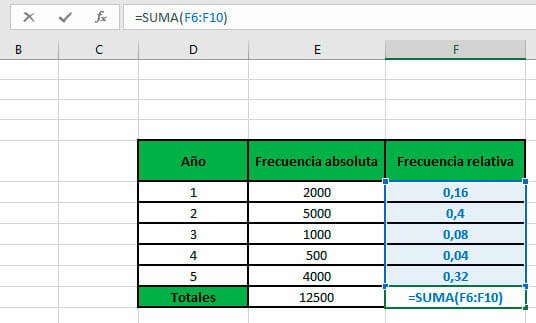
| Año | Frecuencia absoluta | Frecuencia relativa |
| 1 | 2000 | 2000 / 12500 = 0,16 |
| 2 | 5000 | 5000 / 12500 = 0,4 |
| 3 | 1000 | 1000 / 12500 = 0,08 |
| 4 | 500 | 500 / 12500 = 0,04 |
| 5 | 4000 | 4000 / 12500 = 0,32 |
| Totales | 12500 | 1 |
Hecho este análisis, los investigadores pueden emprender estrategias de prevención, con el fin de reducir la tasa de casos y preparar los recursos para el aumento o disminución de los mismos.
Ejemplo de frecuencia relativa con variable continua
En programación, se suele brindar una gran importancia a la velocidad con la que un programa es capaz de realizar cálculos complejos. Con este fin, diversos profesionales diseñaron un software capacitado para resolver problemas físicos avanzados. Para determinar su nivel de optimización, se le solicitó al mismo resolver un caso 10 veces, obteniendo los siguientes resultados.
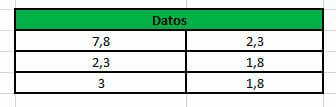
| 6,3 | 2,2 | 4,4 | 4,4 | 6,5 |
| 3,1 | 4,4 | 10 | 4,4 | 3,1 |
Es decir, el tiempo máximo y mínimo que fue necesario para que el programa resolviera el problema fueron de 9,9 y 2,2 segundos, respectivamente.
En este caso, se deben calcular los siguientes valores:
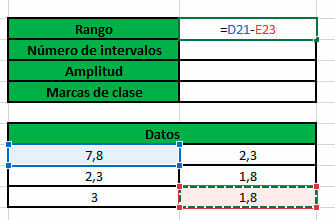
- Rango: es la diferencia entre el mayor de los datos y el menor. Por lo tanto, R = 10 – 2,2 = 7,8.
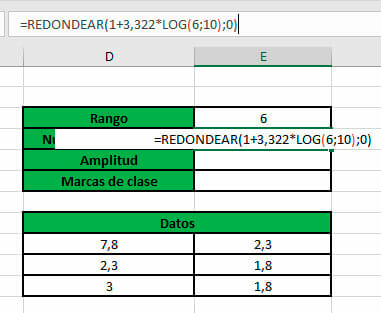
- Número de intervalos: es la cantidad de intervalos en los que se deben agrupar los datos. Este se calcula mediante la Regla de Sturges, es decir K = 1 + 3,322 Log n, donde n es el número de datos. Por lo tanto K = 1 + 3,322 Log 10 = 4 (aproximadamente).
- Amplitud: es el tamaño del intervalo. Se calcula mediante A = R / K. En este caso, A = 7,8 / 4 = 2 (aproximadamente).
- Marcas de clase: son el promedio resultante entre el límite mayor y menor del intervalo. Esto se muestra en la tabla de frecuencias.
Los programadores, finalmente, diseñan la siguiente tabla de frecuencias:
| Tiempo | Marcas de clase | Frecuencia absoluta | Frecuencia relativa |
| [2,2 – 4,2) | (2,2 + 4,2) / 2 = 3,2 | 3 | 3 / 10 = 0,3 |
| [4,2 – 6,2) | (4,2 + 6,2) / 2 = 5,2 | 4 | 4 / 10 = 0,4 |
| [6,2 – 8,2) | (6,2 + 8,2) / 2 = 7,2 | 2 | 2 / 10 = 0,2 |
| [8,2 – 10,2) | (8,2 + 10,2) / 2 = 9,2 | 1 | 1 / 10 = 0,1 |
| Totales | 10 | 1 |
A partir de lo anterior, se puede observar que la duración del cálculo se encuentra, mayoritariamente, en un intervalo de [4,2 – 6,2) segundos. Con esta información, los programadores pueden comparar los diferentes tiempos e implementar estrategias de optimización del programa.
Gráfica de frecuencia relativa
Generalmente, la frecuencia relativa se representa mediante un diagrama de columnas, aunque, en algunos casos, los investigadores pueden optar por implementar un diagrama de barras o un histograma. En este caso, utilizaremos el primer tipo de gráfico, con el fin de que observes de qué manera se puede visualizar esta magnitud estadística.
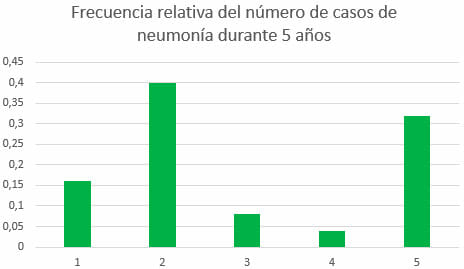
Existen otro tipo de gráficos estadísticos que, aunque no se utilizan para representar frecuencias en general, se pueden utilizar para visualizar la proporción, relación o porcentaje que ocupa una magnitud dentro de un conjunto. Entre estos se cuentan los gráficos circulares o gráficos de pastel.
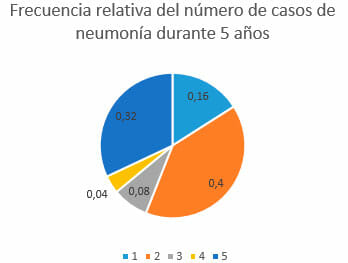
Como se puede observar, este último gráfico permite tener una visión más amplia respecto a las respectivas proporciones de las frecuencias.
¿Cómo calcular la frecuencia relativa en Excel?
Tanto académicos, como profesionales y estudiantes deben utilizar, de manera recurrente, diversos programas informáticos, con el fin de realizar diferentes tareas y obtener resultados precisos. Uno de estos programas es Microsoft Excel, el cual resulta especialmente útil en estadística, tanto por sus funciones matemáticas y estadísticas, como por las herramientas que brinda a la hora de ordenar datos.
En este caso, Excel puede ser un importante apoyo para realizar los cálculos relacionados a la frecuencia relativa. Por esta razón, te enseñaremos cómo hacerlo paso a paso:
- En primera instancia, se debe diseñar una tabla de frecuencias, con el fin de organizar los datos y tener un mayor control sobre los cálculos a realizar.
- Ahora, debemos aplicar la respectiva fórmula de Excel para calcular la frecuencia relativa. Para ello, escribimos lo siguiente en la barra de fórmulas, que se muestra en la parte superior de la imagen.
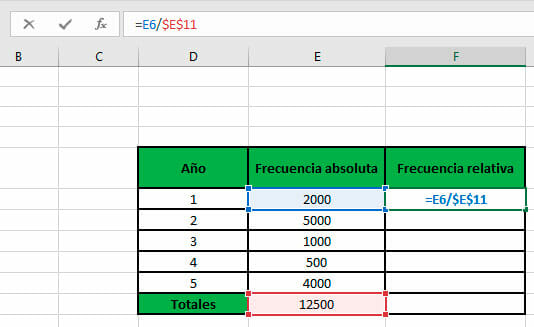
En este caso, se debe emplear una referencia absoluta respecto a la celda que contiene el tamaño de la muestra, pues al encontrarse en un rango diferente, los valores cambiarán al copiar la fórmula para las demás filas. Esto se hace añadiendo el símbolo $ precediendo el indicador de columna y fila, como se muestra en la imagen.
- Para validar que el cálculo se haya realizado correctamente, solo debes implementar la función SUMA, seleccionando el rango de celdas a sumar.
- En caso de que estés trabajando con variables continuas, te puede resultar útil saber cómo aplicar cada una de las fórmulas para diseñar la tabla de frecuencias. A continuación, te mostraremos cómo hacerlo:
- Es recomendable organizar los datos continuos en una tabla, con el fin de operar con ellos posteriormente.
- El rango solo supone una resta entre el mayor y el menor de los datos, por lo que solo debes seleccionar las respectivas celdas y restar sus valores.
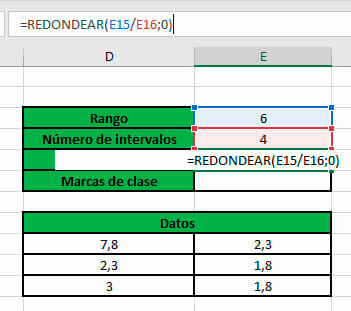
- Para calcular el número de intervalos, es necesario utilizar la función REDONDEAR (número;num_decimales), para aproximar el valor a un número exacto. En el argumento número, escribimos la fórmula correspondiente y, para calcular el logaritmo, empleamos la función LOG.
- Por último, para calcular la amplitud, utilizamos nuevamente la función REDONDEAR y seleccionamos las celdas de los dos anteriores resultados para dividirlos.
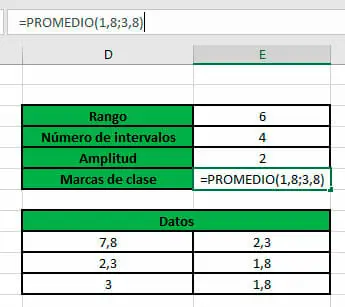
- En el caso de las marcas de clase, estas se pueden calcular mediante la función PROMEDIO. Únicamente, debes seleccionar el rango de cerdas a promediar o escribir los valores.
Conclusiones y recomendaciones
La estadística conserva una estrecha relación con todos los campos del conocimiento y, ciertamente, aporta información relevante para el progreso de los resultados de los mismos. Todos estos tipos de análisis son de suma importancia para conocer el comportamiento y evolución del mundo y de todos sus ámbitos.
Conocer todos estos términos puede mejorar, significativamente, tu trabajo, en cualquiera que sea el área en el que te desempeñes. Asimismo, la estadística es una importante fuente de soluciones, pues a partir de este tipo de estudios, se pueden implementar estrategias y optimizar los procesos.
Utilizar herramientas informáticas para llevar a cabo estas tareas puede resultar un importante progreso. Microsoft Excel es uno de los softwares más completos para realizar cálculos, ordenar datos, diseñar bases de datos, entre otras muchas actividades.
En Excel Para Todos esperamos que puedas mejorar, constantemente, mediante el aprendizaje e implementación de las herramientas que Excel puede ofrecer. Es por ello que hemos preparado una serie de cursos de Excel con los cuales podrás aprender cómo utilizar esta herramienta sin necesidad de que tengas conocimientos o no sobre la misma.
Te recomendamos visitar nuestro blog, donde podrás encontrar artículos similares a éste, tales como: