Frecuencia acumulada
La frecuencia es una de las magnitudes más importantes en los estudios estadísticos, pues permite conocer la recurrencia con que un fenómeno o evento ocurre en un contexto determinado. Esto brinda a los investigadores un amplio campo de acción para tomar decisiones relevantes e implementar estrategias a futuro. Dentro de este análisis de frecuencias, se tiene en cuenta la frecuencia acumulada.
En este artículo te explicaremos de qué se trata la frecuencia acumulada, cuál es su fórmula y la manera en qué se debe calcular, así como algunos ejemplos que te pueden ayudar a comprender de mejor manera este concepto.
¿Qué es la frecuencia acumulada?
La frecuencia acumulada se refiere a la suma recursiva o sucesiva de las frecuencias obtenidas a partir del análisis de una población o muestra. Se le denomina acumulada debido a que los resultados de las sumas se acumulan hasta que se opera con la última de las frecuencias.
Este tipo de análisis de frecuencia se realiza mediante una tabla de frecuencias, en donde se incluyen las variables, ordenadas de mayor a menor si se tratan de variables cuantitativas, con sus respectivas frecuencias.
Tipos de frecuencia acumulada
En los análisis de frecuencias, se suelen considerar diversos tipos con el fin de representar la información de una manera u otra. Estos son la frecuencia absoluta, la frecuencia relativa y la frecuencia porcentual. Cada uno de ellos supone, asimismo, una frecuencia acumulada.
Frecuencia absoluta acumulada
La frecuencia absoluta es la cantidad de veces que un fenómeno, representado por una variable, se repite en un grupo poblacional. De esta manera, la frecuencia absoluta acumulada se obtiene de la siguiente manera:
| Frecuencia absoluta | Frecuencia absoluta acumulada |
| 2 | 2 |
| 3 | 2 + 3 = 5 |
| 4 | 5 + 4 = 9 |
| 7 | 9 + 7 = 16 |
La última de las frecuencias absolutas acumuladas debe ser igual al tamaño muestral o al tamaño de la población analizada.
Frecuencia relativa acumulada
La frecuencia relativa es la fracción que ocupa la frecuencia absoluta dentro del total. En otras palabras, es la relación que conserva una frecuencia respecto a las demás. La frecuencia relativa acumulada, por su parte, se obtiene así:
| Frecuencia relativa | Frecuencia relativa acumulada |
| 0,1 | 0,1 |
| 0,2 | 0,1 + 0,2 = 0,3 |
| 0,3 | 0,3 + 0,3 = 0,6 |
| 0,4 | 0,6 + 0,4 = 1 |
Dado que la frecuencia relativa representa una fracción, la última de las frecuencias relativas acumuladas debe ser igual a 1, es decir, a la unidad.
Frecuencia porcentual acumulada
La frecuencia porcentual es el porcentaje que ocupa la frecuencia absoluta respecto al total. También se puede definir como la frecuencia relativa expresada en porcentaje. En este caso, la frecuencia porcentual acumulada se calcula de la siguiente forma:
| Frecuencia porcentual | Frecuencia porcentual acumulada |
| 10% | 10% |
| 20% | 10% + 20% = 30% |
| 30% | 30% + 30% = 60% |
| 40% | 60% + 40% = 100% |
Así como la última de las frecuencias relativas acumuladas es igual a 1, la última de las frecuencias porcentuales acumuladas es igual a 100%.
Símbolo de la frecuencia acumulada
El símbolo que representa a la frecuencia acumulada depende del tipo de frecuencia al cual se hace referencia. De esta manera, los símbolos son los siguientes:
- Frecuencia absoluta acumulada: F¡.
- Frecuencia relativa acumulada: Hi.
- Frecuencia porcentual acumulada: Hi%.
Como se puede observar, cada uno de los símbolos de las frecuencias acumuladas son, en realidad, el mismo que se utiliza para representar los distintos tipos de frecuencias, pero en mayúscula.
Fórmula de la frecuencia acumulada
La fórmula de la frecuencia acumulada se expresa como la sumatoria de las frecuencias hasta n, donde n es el número de la frecuencia evaluada:
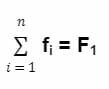
Esto se puede interpretar de la siguiente manera:
Fi = ((((f1) + f2) + f3) + …) + fi.
Así, se dice que las frecuencias se acumulan y, por lo tanto, se deben resolver las operaciones que se encuentran entre los paréntesis más internos, de manera sucesiva.
¿Cómo calcular la frecuencia acumulada?
El método empleado para calcular la frecuencia acumulada se expresa como una serie de pasos recursivos, lo que se puede ilustrar mediante la siguiente tabla:
| F1 | f1 |
| F2 | F1 + f2 = f1 + f2 |
| F3 | F2 + f3 = f1 + f2 + f3 |
| … | … |
| Fi | Fi + fi = f1 + f2 + f3 + … + fi |
Ejemplo de frecuencia acumulada
Existen una gran cantidad de casos en los que las frecuencias acumuladas deben ser calculadas para obtener información precisa acerca de una población. Un breve ejemplo de ello es el siguiente:
Al terminar el período de exámenes de un curso de matemáticas, el profesor encargado decide llevar a cabo un análisis de frecuencias con el fin de conocer la cantidad de veces que una calificación fue obtenida por los 35 estudiantes del grupo. En este caso, se tienen los siguientes datos:
| Nota | Frecuencia absoluta | Frecuencia absoluta acumulada | Frecuencia relativa | Frecuencia relativa acumulada |
| A | 3 | F1 = 3 | 0,1 | H1 = 0,1 |
| B | 10 | F2 = 3 + 10 = 13 | 0,3 | H2 = 0,1 + 0,3 = 0,4 |
| C | 15 | F3 = 13 + 15 = 28 | 0,4 | H3 = 0,4 + 0,4 = 0,8 |
| D | 3 | F4 = 28 + 3 = 31 | 0,1 | H4 = 0,8 + 0,1 = 0,9 |
| F | 4 | F5 = 31 + 4 = 35 | 0,1 | H5 = 0,9 + 0,1 = 1 |
| Total | 35 | Ftotal = 35 | 1 | Htotal = 1 |
Con lo anterior, se puede observar que el número de estudiantes que han obtenido una calificación A (Sobresaliente), sólo representan el 0,1 del total de estudiantes, así como aquellos que obtuvieron calificaciones de D y F. La mayoría de estudiantes, según la tabla, obtuvieron notas de B y C.
Gráfica de frecuencia acumulada
La distribución de frecuencias, en general, se representa mediante diagramas de columnas, diagramas de barras o, en caso de que los datos estadísticos se encuentren agrupados en intervalos, histogramas. Utilizar estos tipos de gráficos estadísticos puede resultar útil al momento de realizar posteriores análisis y observaciones.
A continuación, veremos un ejemplo de diagrama de barras combinado que representa la frecuencia acumulada de un grupo de datos:
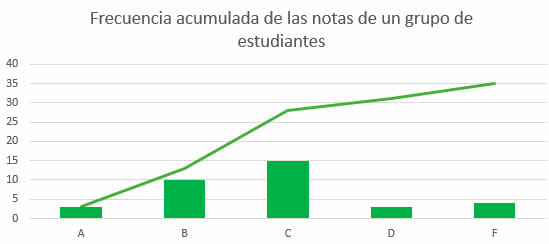
Como se puede observar, las frecuencias aumentan de manera progresiva y proporcional, pues los resultados anteriores se acumulan, sumándose, recursivamente, con los demás hasta alcanzar el total. Esta progresión también se puede representar mediante únicamente un gráfico de líneas.
¿Cómo calcular la frecuencia acumulada en Excel?
Microsoft Excel se ha posicionado como uno de los programas informáticos más importantes en el ámbito profesional y académico, debido a las diversas funciones y herramientas que ofrece para la organización de los datos, la aplicación de fórmulas matemáticas y la representación de la información mediante gráficos.
Emplear Excel para diseñar tablas de frecuencias y llevar a cabo sus respectivos cálculos puede resultar bastante útil, por lo que te enseñaremos, en unos cuantos pasos, de qué manera calcular la frecuencia acumulada en Excel.
- En este caso, se tiene una tabla de frecuencias donde las frecuencias absolutas, relativas y porcentuales ya fueron calculadas. Ahora, la primera frecuencia acumulada siempre es igual a la primera frecuencia a la que hace referencia. Por lo tanto, se obtiene lo siguiente:
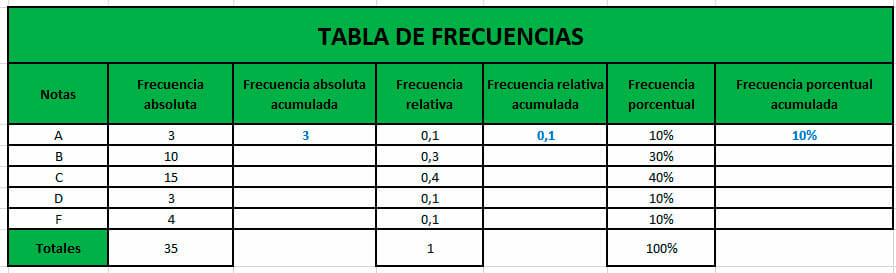
- La frecuencia relativa se puede expresar como la suma entre el resultado anterior y la frecuencia actual. Para ello, escribimos en la barra de fórmulas la siguiente operación:
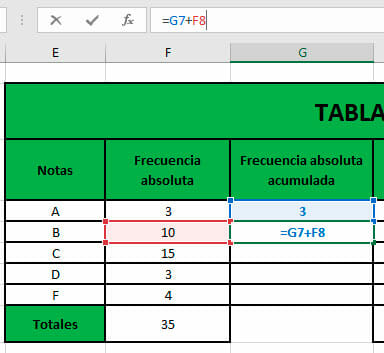
De esta manera, el resultado de la celda anterior se sumará con la frecuencia que se encuentra en la fila en la que se está aplicando la fórmula de Excel.
- Posteriormente, solo debes copiar la fórmula para las demás celdas, lo cual se hace, haciendo click sobre el vértice inferior derecho de la celda actual y moviendo el ratón hacia la última celda. Excel se encargará de seleccionar las celdas correspondientes para los demás resultados.
- Por último, se aplica la misma operación con los demás tipos de frecuencias seleccionando sus respectivas celdas.
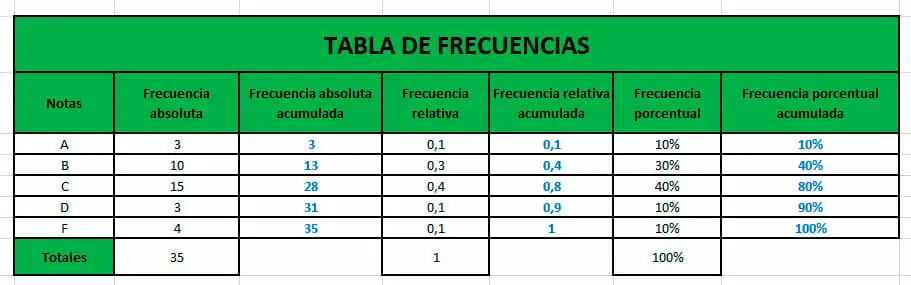
Conclusiones y recomendaciones
La distribución de frecuencias es uno de los parámetros más importantes de la estadística descriptiva, debido a su capacidad de brindar información respecto a la cantidad de veces que un fenómeno se repite en un espacio de tiempo, lugar o grupo determinado.
Este análisis se hace en un amplio rango de campos del conocimiento, como lo son la climatología, la sociología e, incluso, la inteligencia artificial con el fin de determinar la frecuencia de las respuestas o palabras más usadas en ciertos contextos.
El acompañamiento por parte de las tecnologías en este tipo de labores optimiza, en gran medida, los análisis y permite obtener resultados confiables, de manera rápida y precisa. Es por esta razón que Microsoft Excel es una de las herramientas más utilizadas en este medio, pues permite realizar una gran cantidad de tareas con unos cuantos conocimientos, los cuales pueden ampliarse para obtener mejores resultados.
En Excel Para Todos tenemos como meta que puedas aprovechar todas las funciones y herramientas que Excel te puede ofrecer para que mejores tu rendimiento en tu trabajo y, por lo tanto, adquieras mejores beneficios del mismo. Por ello, hemos desarrollado una serie de cursos de Excel con los cuales podrás aprender, de manera sencilla y agradable, cómo manejar este programa, sin necesidad de que no tengas conocimientos sobre él.
Puedes visitar más artículos como este en nuestro blog, donde podrás encontrar temas relacionados a las Finanzas, la Contabilidad y la Administración de proyectos. Te recomendamos echar un vistazo a las siguientes entradas: