Muestreo Estratificado
Los diversos elementos que conforman a una población pueden presentar ciertas similitudes y diferencias que, al no considerarlas, pueden afectar el resultado de la investigación en curso. En este tipo de casos, se suele realizar una división de los individuos a partir de sus características, proceso que hace parte del muestreo estratificado.
El muestreo estratificado es uno de los muestreos probabilísticos implementados en las investigaciones de estadística inferencial. En este artículo, te explicaremos de qué se trata, cómo lo puedes aplicar y qué debes tener en cuenta al hacerlo.
¿Qué es el muestreo estratificado?
El muestreo estratificado es un método implementado en estadística en el que la población se divide en estratos homogéneos, es decir, grupos de elementos que cuentan con una característica en común. De esta manera, cada clasificación obtiene una representación significativa dentro de la muestra de la investigación.
Cada estrato ocupa un porcentaje de la población total y, por lo tanto, se busca que el número de elementos de cada grupo cuente con la cantidad de representantes necesarios para que la muestra sea equitativa.
¿Cuándo se utiliza el muestreo estratificado?
Este tipo de muestreo probabilístico se utiliza en poblaciones cuyos elementos son heterogéneos, es decir, que no cuentan con un patrón o característica general que los identifique. En estos casos, es necesario que el investigador divida a la población en grupos que reúnan las partes similares entre sí, buscando representar, equitativamente, a todos en la muestra.
En este mismo contexto, el muestreo estratificado se utiliza para estudiar el comportamiento de los subgrupos dentro de la población y sus relaciones.
Características del muestreo estratificado
- La población se divide en estratos, cuyos elementos cuentan con una característica en común.
- Es uno de los muestreos estadísticos más utilizados, debido a la facilidad que brinda al investigador de conocer la población.
- El cálculo del tamaño de muestras se puede hacer de manera proporcional o no.
- Estima el tamaño de la muestra de una población a partir de los costos de una investigación.
Tipos de muestreo estratificado
Según el tamaño de la muestra obtenido para cada estrato, el muestreo estratificado se clasifican en los siguientes tipos:
Muestreo estratificado proporcional
También denominado muestreo por afijación proporcional, se refiere a que el tamaño de la muestra para cada estrato es proporcional al porcentaje que ocupa dicho grupo en la población. La fórmula para este tipo de muestreo es:
n_estrato = n (número de elementos del estrato / tamaño de la población)
donde n es el tamaño de la muestra.
Muestreo estratificado no proporcional
Conocido, de igual manera, como muestreo por afijación igual, los tamaños muestrales de cada estrato son iguales, sin considerar la proporción de los mismos con respecto a la población. En este caso, la operación a realizar es:
n_estrato = n / número de estratos.
Muestreo estratificado óptimo
En este caso, se consideran los costos de la investigación al calcular el tamaño de la muestra, buscando reducir el margen de error con respecto a un costo. La fórmula para este caso es:
n = (Costo total de la investigación – Costo fijo) / Costo unitario por estrato.
Muestreo Estratificado por conglomerados
La población se divide en conglomerados, los cuales se encuentran conformados de manera natural y previamente a la investigación. Por lo tanto, los grupos pueden presentar cierta heterogeneidad al no considerarse las características evidentes, sino su clasificación existente en la realidad.
En este caso, la muestra no considera la totalidad de los grupos definidos en la investigación, sino que se realiza una selección aleatoria de los conglomerados y, posteriormente, otra selección dentro de los mismos.
Dependiendo del número de selecciones a realizar, el muestreo estratificado por conglomerados se divide en:
- Muestreo por conglomerados de una sola etapa: solo se realiza una selección, en la que se escogen los conglomerados de manera aleatoria, de manera que todos los elementos que pertenecen a los mismos son representados en la muestra.
- Bietápico: se seleccionan los conglomerados y, posteriormente, se aplica otro tipo de muestreo probabilístico para seleccionar algunos de los elementos de cada uno de ellos.
- Polietápico: en este caso, se realizan más de dos selecciones, pues los conglomerados contienen subgrupos, los cuales también se dividen en otros, de manera que se aplica un muestreo para cada uno de ellos.
De acuerdo a algunas definiciones, el muestreo por conglomerados es un tipo de muestreo probabilístico similar al muestreo estratificado, pero no pertenece a este último. Sin embargo, cuentan con ciertas similitudes, a partir de las cuales se puede hacer una sola clasificación entre los dos métodos.
Ventajas y desventajas del muestreo estratificado
Ventajas
- Todos los estratos o grupos de elementos cuentan con una representación significativa en la muestra, lo que brinda resultados más precisos con respecto a la población.
- Permite clasificar los diversos datos de una población, reduciendo la complejidad de la misma a sus partes.
- Abarca cualquier clase de elemento que conforma una población, y considera las características particulares de cada grupo.
- Reduce el margen de error de la investigación.
- Permite conocer la naturaleza de una población.
Desventajas
- Puede resultar costoso debido al trabajo que supone la clasificación de la población en los estratos.
- En poblaciones donde se presente un gran porcentaje de heterogeneidad, la clasificación puede resultar dificultosa. En este caso, la cantidad de estratos supone un grado de complejidad del estudio.
- Se debe considerar tanto la proporción como las características de los estratos de manera previa.
¿Cómo se realiza el muestreo estratificado?
A continuación describiremos los pasos para realizar el muestreo estratificado:
Definición de la población
La primera etapa de cualquier investigación es identificar el contexto, campo o población de la cual se desea realizar un estudio.
Selección de variables y estratos
La selección del marco muestral debe considerar que los elementos que hacen parte del mismo cuenten con características capaces de representar con la mayor exactitud y relevancia el aspecto objetivo de la investigación. De igual manera, al dividir la población en estratos estos deben incluir datos que cuenten con una característica en común bien definida.
Cálculo del tamaño de la muestra
El tamaño de la muestra se debe calcular considerando ciertos aspectos propios de los elementos de la población y el objetivo de la investigación. Para este tipo de cálculo se aplican las fórmulas del muestreo aleatorio simple. Se debe verificar que la cantidad de datos que conformarán a la muestra sean suficientes para lograr una mayor representatividad.
Selección de la muestra
Este proceso se lleva a cabo, como en todos los muestreos de tipo probabilístico, a partir de un sorteo de números aleatorios, los cuales son asignados a cada elemento de cada uno de los estratos, los cuales son seleccionados para conformar la muestra. El criterio de selección depende del investigador, y se puede realizar mediante el ordenamiento de mayor a menor o viceversa de los datos o mediante otro tipo de conteo.
Recolección de datos
Una vez preparados los recursos y los cálculos pertinentes, los investigadores pueden recolectar los datos que hacen parte del estudio, teniendo en cuenta que deben cumplir con el tamaño de la muestra de cada estrato.
Análisis e interpretación de resultados
La fase final de la investigación se refiere a un proceso de definición de conclusiones a partir de los resultados obtenidos. Esto se puede lograr mediante las diversas fórmulas y herramientas de la estadística descriptiva e inferencial, ramas que permiten representar, gráficamente, el comportamiento de la población y la toma de decisiones.
Cómo hacer un muestreo estratificado en Excel
Microsoft Excel es una excelente herramienta para este tipo de investigaciones, pues permite realizar los cálculos y organizar los datos de manera eficiente. A continuación, te explicaremos cómo hacer un muestreo estratificado fácilmente:
- Antes de iniciar cualquier tipo de cálculo, es recomendable utilizar una tabla para organizar los datos que hacen parte del estudio. Esto facilita el uso de funciones matemáticas y permite comprender el contexto en el que se encuentra la información.
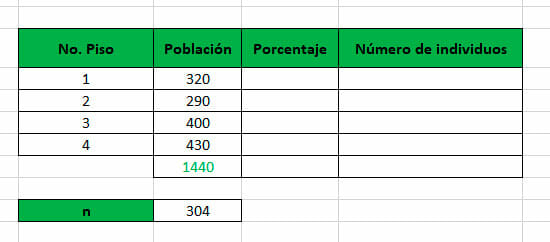
- Para calcular los porcentajes a los que corresponde cada estrato con respecto a la población, se divide el número de individuos que hacen parte del estrato entre la totalidad de personas. Esta fórmula se puede escribir en la barra de fórmulas de Excel.
Para aplicar la operación en las demás celdas, se debe utilizar el valor absoluto de la celda en la que se encuentra, en este caso, el tamaño de la población, de manera que este dato sea constante. Para ello, se debe escribir un signo $ antes de las etiquetas de columna y fila, como se observa en la imagen.
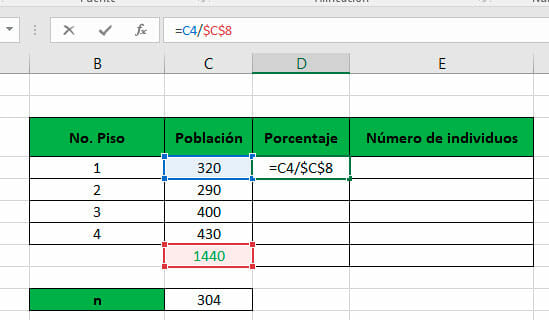
De esta manera, al arrastrar la función aplicada en la primera celda hacia las demás, la operación se realizará correctamente.
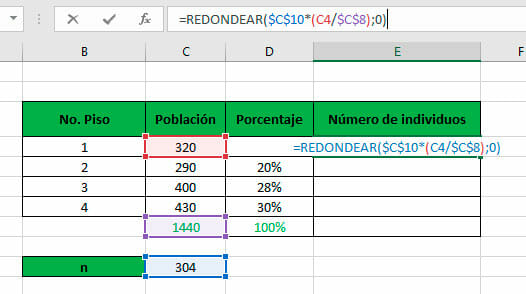
- La cantidad de elementos o individuos por estrato que harán parte de la muestra se puede calcular utilizando, nuevamente, el valor absoluto de la celda a la que se hace referencia, en este caso, tanto del tamaño de la muestra como de la población, y una simple operación de multiplicación y división.
Dado que para el presente tutorial se está calculando una muestra conformada por individuos, esta no puede ser decimal. Para evitar esto, podemos utilizar la función matemática REDONDEAR, cuya sintaxis es:
=REDONDEAR(número; núm_decimales). En este caso, el segundo argumento debe ser igual a 0.
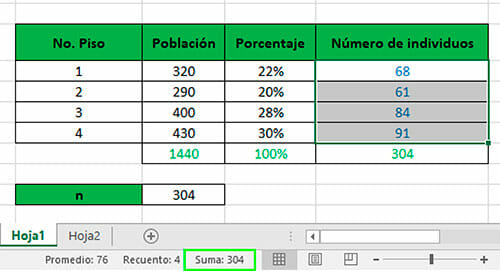
- La suma de los resultados anteriores debe ser igual al tamaño de la muestra, cosa que se puede comprobar seleccionando el rango de celdas y, en la barra de estado de la parte inferior, se mostrará el total de la operación.
Ejemplo de muestreo aleatorio estratificado
La gerencia de un conjunto residencial requiere hacer un estudio de viabilidad de un proyecto en un edificio, conformado por cuatro pisos, con el fin de buscar la aprobación de los habitantes. De acuerdo a los registros de la administración, el edificio cuenta con 90 residentes. Por lo tanto, la empresa opta por usar un muestreo estratificado, considerando cada una de las manzanas que conforman la zona. Se calcula un tamaño muestral de 10 personas.
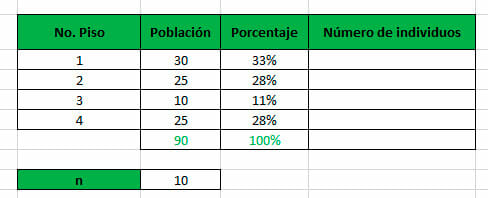
Al calcular el tamaño muestral, proporcionalmente, para cada estrato, utilizando la fórmula n * (tamaño del estrato / tamaño de la población), se obtiene que:
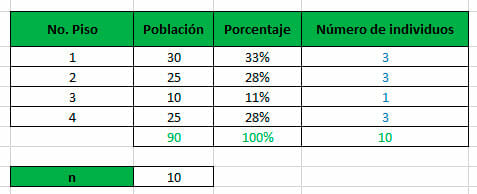
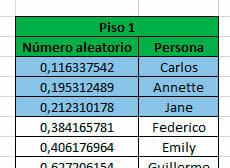
Una vez hecho esto, la empresa realiza un sorteo a partir de números aleatorios, los cuales son asignados a cada una de las personas que habitan en cada uno de los pisos. El orden de selección se realiza de menor a mayor, de manera que los individuos que cuentan con los números aleatorios menores fueron seleccionados para la muestra.
En el caso del piso 1, se seleccionaron las siguientes personas:
Consideraciones al realizar muestreo estratificado
- Tanto el muestreo estratificado como el muestreo sistemático parten de la base del muestreo aleatorio simple, añadiendo otros cálculos y técnicas. Por lo tanto, al implementar cualquier tipo de muestreo probabilístico, se deben utilizar las mismas fórmulas para calcular el tamaño de la muestra y seleccionar los elementos de la misma.
- Los estratos deben encontrarse en un mismo rango o nivel de clasificación. Por ejemplo, en una investigación donde exista un estrato para perros y otro para gatos, no puede existir otro para gatos de color naranja o perros pequeños, pues es un clasificación subyacente de los dos principales grupos.
- Dependiendo de la clase de variables que conforman la población y el tamaño de esta última, se debe utilizar una u otra fórmula para calcular el tamaño de la muestra. Cabe mencionar que las variables pueden ser cualitativas o cuantitativas, mientras que las poblaciones pueden ser finitas o infinitas.
Conclusiones y recomendaciones
Desde las civilizaciones más antiguas, la estadística ha supuesto una de las ramas más importantes para la gestión de grandes poblaciones. Es por esta razón que esta ciencia se ha posicionado como una herramienta eficaz, tanto en el pasado como en el presente, para la administración del Estado, de donde proviene su nombre, y las empresas. Su importancia radica, por lo tanto, en la seguridad que brinda al tomar decisiones significativas.
Los diversos tipos de muestreo son, en este contexto, un gran apoyo para la estimación del comportamiento y estado de un gran conjunto de datos. Saber implementarlos correctamente facilita las investigaciones y reduce los costos de las mismas. Por ello, el aprendizaje respecto a la aplicación de estas técnicas junto a la estadística en general supone un enorme progreso.
En Excel Para Todos sabemos que el constante aprendizaje es la base para todo avance y, por esta razón, te invitamos a visitar nuestro blog, donde podrás encontrar artículos y tutoriales similares a este, así como nuestros cursos de Excel, mediante los cuales conseguirás saber utilizar este programa para que obtengas mejores resultados y optimices tus tareas.
Nuestras plantillas gratuitas y premium de Excel te ayudarán a realizar diversas tareas relacionadas a las finanzas y la contabilidad, garantizando que realices tus cuentas de manera segura y precisa.